Коаксиальный волновод

Общее для волн Т-типа 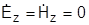. Такое возможно, если волна распространяется вдоль направляющей системы без отражений, то есть для любой составляющей решение имеет вид:

.

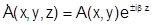Коэффициент фазы и продольное волновое число при этом совпадают:

.

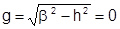Для волн Т-типа (всегда имеется в виду низший тип волны):

,

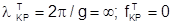т.е. волновод должен пропускать колебания любых частот вплоть до постоянного тока.

В волноводе с волной Т-типа должны быть минимум два проводника разделенных слоем диэлектрика.

Волновой фронт перемещается со скоростью: .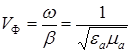

Волны Т-типа не имеют дисперсии.

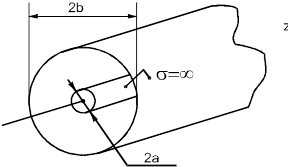Коаксиальный волновод - это два соосных цилиндра.

В однородной материальной среде без зарядов третье уравнение Максвелла 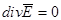будет всегда выполняться, если принять: ;

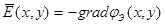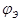- вспомогательная функция - скалярный электрический потенциал.

Знак «-» выбран, чтобы вектор Е начинался на «+» и заканчивался на «-» зарядах (принято в электротехнике).

Подставляем: .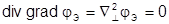

Для коаксиальной линии (в дальнейшем КЛ) удобнее использовать ЦСК.

Из-за полной симметрии волновода 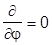двумерное уравнение Лапласа принимает вид:

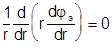или .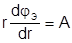

Общее решение этого уравнения: .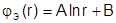

Постоянные А и В следует определять из граничных условий.

Полагаем потенциал наружного проводника равным нулю (заземлён), а внутреннего равным U тогда:

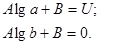
Определяем А и В и получим:

.

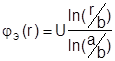Амплитуду вектора Е определим как:

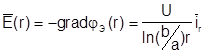, (3.20)

то есть Е имеет только r-ю составляющую и для комплексной амплитуды (диэлектрик без потерь):

.

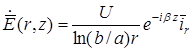Для определения Н используем второе уравнение Максвелла:

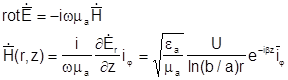
т.е. Н имеет только азимутальную составляющую, а отношение Е к Н в каждой точке пространства равно характеристическому сопротивлению среды, заполняющей коаксиальную линию:

.

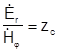Токи на металле имеют только Z составляющую и разное направление на внутренней и внешней трубе, причем их амплитуды равны:

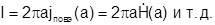
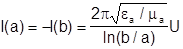
Для коаксиальной линии в отличие от полых волноводов удобно ввести волновое сопротивление:

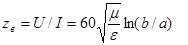(3.21)

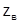(не связано с потерями энергии - это только коэффициент пропорциональности).

Зная Е и Н определим мощность переносимую вдоль оси волновода:

.

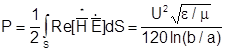Структура поля в коаксиальном волноводе:

Дата добавления: 2014-01-06