Идеальный газ в поле силы тяжести

Уравнение состояния идеального газа

В процессе вывода соотношения (2.6) возникли еще две макроскопические характеристики системы многих частиц — давление P и объем V. Задание температуры, давления и объема определяет состояние системы частиц (тела). Эти величины называются параметрами состояния.

Давление P, объем V и температура, T не являются независимыми величинами. Соотношение, связывающее эти три параметра, вида f (P, V, T) = 0 называется уравнением состояния. Найдем уравнение состояния идеального газа. Подставляя в соотношение (2.6) выражение (2.3), получим

PV = N·k_Б·T. (2.7)

Отметим универсальный характер полученного уравнения: в него не входят никакие величины, характерные для определенного газа, а только числа частиц. Отсюда следует, в частности, что при одинаковых давлении и температуре разные газы, занимающие равные объемы, содержат в них равные числа молекул. Этот закон был установлен ранее опытным путем Авогадро.

Перепишем уравнение состояния в терминах объема, приходящегося на единицу вещества — моль. Один моль — это количество вещества в граммах, численно равное его молекулярному весу. Например, 1 моль кислорода содержит 32 г вещества. Удобство этой единицы измерения состоит в том, что по определению в 1 моле любого вещества содержится одинаковое число молекул, называемое числом Авогадро N_A. Оно равно 6·10²³ молекул. Число молекул в объеме газа можно записать в виде:

N = ν· N_A,

где v — число молей данного вещества в указанном объеме. В этих обозначениях уравнение состояния принимает вид:

PV = v · R · T. (2.8)

Величина R = k_БN_A называется газовой постоянной. Пусть при нагревании газа на 1 К объем, занимаемый 1 молем газа, изменился при неизменном давлении на Δ V. Представляя давление газа в виде P = F / S, а объем сосуда в виде Δ V =, видим, что величина P Δ V = F Δ h есть работа, произведенная газом при его расширении. Таким образом, физический смысл газовой постоянной состоит в том, что она численно равна работе, совершенной 1 молем газа при его нагревании на 1 К при постоянном давлении.

Каково поведение идеального газа в поле внешней силы? Для определенности в качестве внешней силы возьмем хорошо известную силу тяжести mg. Под действием внешней силы механическая система частиц приобретает импульс и перемещается как целое поступательно в направлении силы. В идеальном газе, находящемся во внешнем поле сил, каждая отдельная частица приобретает импульс в направлении силы, а также соответствующую потенциальную энергию. Однако в газе наряду с упорядоченным движением в направлении действия силы существует хаотическое тепловое движение. В результате конкуренции между этими двумя типами движений возникает неравномерное распределение макроскопических параметров: плотности частиц, давления, температуры по объему, занимаемому газом.

Рассмотрим столб газа сечением S, находящийся при постоянной температуре в поле силы тяжести. Выделим слой газа толщиной dz на высоте z и вычислим давление газа на его основания. Давление слоя газа на верхнее и нижнее основания слоя разное — оно различается в результате действия силы тяжести. Очевидно, разность давлений равна весу газа, заключенного в слое, отнесенному к единице площади основания столба.

Пусть разность давлений есть dP. Давление газа с ростом высоты уменьшается, поэтому dP равно весу слоя со знаком минус. Вес газа в объеме слоя dV = dz · S равен ρ· g · dV, где ρ — плотность газа, g — ускорение силы тяжести. Таким образом,

dP = ‑ρ· g · dV / S = ‑ρ· g · dz.

По определению . Выразим отношение N / V с помощью уравнения состояния (2.7), после чего находим:

.

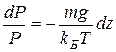Интегрируя это соотношение, получим 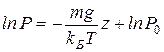, где P₀ — константа, определяемая пределами интегрирования. Окончательно имеем:

. (2.9)

Здесь P₀ — давление при z = 0. т. е. у основания столба. Аналогично с высотой изменяется и плотность частиц

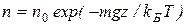. (2.10)

Давление и плотность газа распределены по объему газа неоднородно, они принимают максимальные значения у основания столба и убывают с высотой.

Величина, входящая в показатель экспоненты в формулах (2.9) и (2.10), есть потенциальная энергия частицы в поле тяжести U = mgz -Таким образом, распределение молекул в произвольном потенциальном внешнем поле, в котором частицы обладают потенциальной энергией U (r), может быть описано формулой:

. (2.11).

Эта формула называется распределением Больцмана. Здесь n₀ — плотность частиц в точках пространства, для которых потенциальная энергия принята равной нулю.

Согласно распределению Больцмана число частиц, обладающих определенными значениями потенциальной энергии определяется отношением величины потенциальной энергии U к тепловой энергии частицы k_БT. Чем больше энергия теплового движения, тем более разупорядочена система частиц, значит, тем более однородно распределены частицы в пространстве. В самом деле, если k_БT >> U, 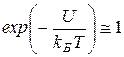, и из формулы (2.11) следует, что n = n₀ при любом значении U. В случае k_БT << U распределение частиц максимально упорядочено: плотность частиц максимальная состоянии с минимальной потенциальной энергией U_min, в то время как плотность частиц в других состояниях равна нулю.

Дата добавления: 2014-01-06