Зависимость по данным

Крупнозернистый

У

Л

Микроуровневыйпараллелизм Параллелизм уровня командПараллелизм уровня потоков

Параллелизм уровня заданий

Мультипроцессорные системы Мультикомпьютерные системы

>

>

Степень гранулярности:

Мелкозернистый >~ Среднезернистый

Параллелизм - это возможность одновременного выполнения более одно арифметико-логической операции. Возможность параллельного выполнения этих операций определяется правилом Рассела, которое состоит в следующем [10].

Программные объекты А и В (команды, операторы, программы) являются независимыми и могут выполняться параллельно, если выполняется следующее условие:

(InB □ ОшА) □ (InA □ OutB) □ (OutA □ OutB) = 0, (2.1)

где In(A) - набор входных, a Out(A) - набор выходных переменных объекта А. Если условие (2.1) не выполняется, то между А и В существует зависимость и они не могут выполняться параллельно.

Если условие (2.1) нарушается в первом терме, то такая зависимость называется прямой. Приведем пример:

A: R = Rl + R2 В: Z = R + С

Здесь операторы А и В не могут выполняться одновременно, так как результат А является операндом В.

Если условие нарушено во втором терме, то такая зависимость называется

обратной:

A: R = Rl + R2 В: Rl = CI + С2

Здесь операторы А и В не могут выполняться одновременно, так как выполнение В вызывает изменение операнда в А.

Наконец, если условие не выполняется в третьем терме, то такая зависимость называется конкуренционной:

A: R = Rl + R2 В: R = CI + С2

Здесь одновременное выполнение операторов дает неопределенный результат.

Увеличение параллелизма любой программы заключается в поиске и устранении указанных зависимостей.

Наиболее общей формой представления этих зависимостей является информационный граф задачи (ИГ). Пример ИГ, описывающего логику конкретной задачи, дан на рис.2.1. В свое первоначальной форме ИГ, тем не менее, не используется ни математиком, ни программистом, ни ЭВМ.

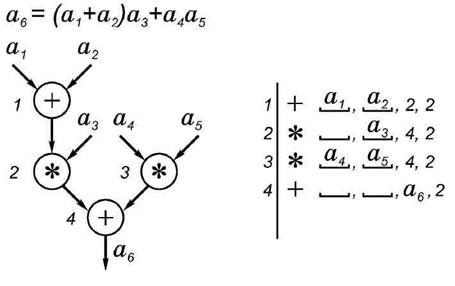
Рис.2.1. Информационный граф математического выражения и порядок выполнения операций в выражении.

Более определенной формой представления параллелизма является ярусно-параллельная форма (ЯПФ): алгоритм вычислений представляется в виде ярусов, причем в нулевой ярус входят операторы (ветви), не зависящие друг от друга, в первый ярус — операторы, зависящие только от нулевого яруса, во второй — от первого яруса и т. д.

Для ЯПФ характерны параметры, в той или иной мере отражающие степень параллелизма метода вычислений: bi - ширина i-ro яруса; В - ширина графа ЯПФ (максимальная ширина яруса, т. е. максимум из Ы, i = 1, 2,...); Ь — длина яруса (время операций) и L длина графа; г — коэффициент заполнения ярусов; 8 — коэффициент разброса указанных параметров и т. д.

Дата добавления: 2014-01-06