E1 » 8,7 эВ

Чтобы описать волновые свойства нужно ввести волновую функцию. Эта волновая функция y(x,y,z,t). |y(x,y,z,t)|2 – вероятность обнаружить частицу в данной точке пространства в данный момент времени. Существенным свойством такого квантового описания является его вероятностный характер. Т. е. о том, что определенная система находится в том или ином состоянии можно говорить только с определенной долей вероятности.

Рассмотрим несколько примеров систем.

У этой волновой функции есть свойство суперпозиции:

y = y₁ + y₂

Если система может находиться в каких-то нескольких состояниях, то ее общее состояние может описываться на основе сумы волновых функций, которыми обладает система. Проиллюстрируем это.

Пример 1: свободная частица, о которой мы знаем, что она имеет импульс p₀. В соответствии с формулой мы можем приписать ее вполне определенную длину волны:

l₀ = 2ph/p₀

Известно, что волна, длина которой не меняется, это монохроматическая волна. Про координаты этой частицы мы ничего не знаем. Попробуем найти волновую функцию этой частицы. Поскольку это волна, то можно считать, что волновая функция должна изменятся по закону синуса или косинуса y = Acos(k₀x – wt), где А – какой-то коэффициент. Тогда вероятность нахождения частицы |y|² = A²cos²(…). Эта функция содержит нули и нам не подходит потому, что свободная частица равновероятна в любой точке. Подходит такая функция y = Ae^i(k0^{x – wt)}. Эта волновая функция комплексная: |y|² = y^**y = A².

Пример 2:

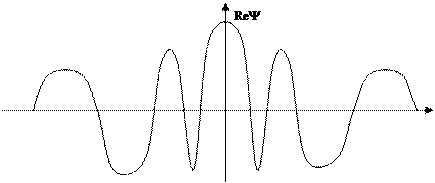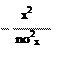Зададим распределение волновой функции только на конечном участке.

y(x) = Ae *e^ikox

А – амплитуда. Это гармоническая функция. Амплитуда по х ограничена s_x. Это известное Гауссово распределение. С вероятностью 50 % она находится вблизи точки х = 0. Мы знаем, что по х она находится в пределах от –s_x до +s_x. Что мы знаем о скорости этой частицы или о ее импульсе? Разложим волновую функцию в интеграл Фурье.

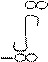y(x) = B(k)e^ikxdk

Найдем коэффициенты разложения

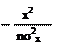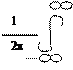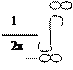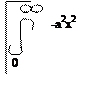B(k) = y(x)e^-ikxdx = Ae * e^-i(k-k0)xdx = e cosmxdx =

		sx

p

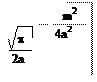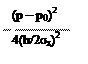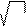
e = A e

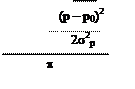
A²s²_xe = |B(p)|²

Оказывается, что импульс тоже распределен по закону Гаусса:

s_p = h/2s_x

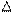
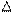
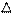
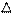s_ps_x = p x = h/2 - это в случае распределения Гаусса. А в случае любого другого распределения будет p x > h/2. Это так называемое соотношение неопределенности, которое означает, что чем точней мы мерим координату, тем меньше мы знаем об импульсе и о скорости и наоборот. Это соотношение можно преобразовать в следующее:

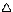
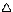
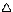
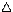
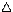
p x = m v * v t = mv v t = E t > h/2

Электрон характеризуется таким образом: чем мы больше хотим о нем знать с какой-то его одной стороны, тем меньше о нем знаем с другой, а в целом никогда ничего не можем сказать определенного.

Пример 3. Помещаем электрон в ящик с бесконечными стенками, т.е. если мы туда электрон забросим, то он там и будет. Мы не знаем, что с ним происходит, но точно знаем, что он там. Попытаемся объяснить, что с ним там происходит. Электрон в атоме водорода притягивается к протону и не отрывается от него – аналогия.

За стенки электрон выйти не может. Абсолютно достоверно можно утверждать, что электрон в ящике покоиться не может. Доказательство этого утверждения: если бы он там покоился, тогда можно было бы сказать, что у него импульс равен 0, т.е. вполне определенный импульс, а значит, он размазан по пространству. А он в ящике – он не может быть размазан. Т.е. он там движется. С ним соотносится волновая функция. Вероятность распределения электрона за пределы этого ящика равна 0. То естественно здесь должно оказываться либо пол волны, либо целая волна, либо 3 полу периода длины волны. Вероятность распределения должна быть непрерывна. Мы можем утверждать, что длина волны может иметь только строго определенные значения. А раз длина волны дискретна, значит, импульс дискретен, значит и энергия дискретна. Т.е. частица в замкнутом пространстве не может иметь любую энергию, а только строго определенную.

y₊ = Be^ikx-iwt

y_- = -Be^-ikx-iwt

Суммарная волновая функция y = y₊ + y_- = Be^ikx-iwt – Be^-ikx-iwt = 2iBsinkx_*e^-iwt. Если оставить только пространственную часть, обозначить А = 2iВ, то получим волновую функцию y = A_*sinkx. Ширина ящика L. Обязательно должно быть kL = np – это условие того, что на ширине этой потенциальной ямы укладывается полное число полуволн. n= 1, 2, …

k_n = pn/L – только такие значения может принимать волновой вектор. Соответственно импульс может принимать значения

p_n = pnħ/L

энергия – E_n = p²/2m = p²h²n²/2mL². Это уровни энергии, которыми может обладать частица в ящике.

Возьмем ящик шириной в 2А. Ангстрем – это размер атома. k=2_*10^-10м. Первый уровень энергии

E₂» 35 эВ

n – это квантовое число для этой частицы в ящике. Если мы частицу поместили в замкнутое пространство, что все равно, что мы частицу поместили в атом, то у нас получается дискретный спектр энергий.

Если у нас яма не с бесконечными стенками, а с конечными

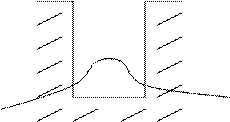то тоже можно решить эту задачу, но это будет немного сложней. Мы должны будем учесть, что какая-то вероятность за пределами существует. Вероятность, что он оттуда ускользнет, возрастает с уменьшением длины стенок.

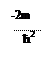Атом водорода.

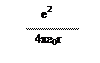Уравнения Шредингера ΔΨ = (E – U(r))Ψ

U(r) = -

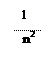Это потенциал взаимодействия электрона с протоном. Подставляем его в уравнение и решаем уравнение. Поскольку задача сферически симметрична, то делаем замену переменных на сферические координаты. За счет сферической симметрии у нас задача распадется на 3 отдельные задачи, и у нас будет квантование энергии по всем трем координатам. Но энергия зависит от расстояния до ядра, но она не зависит от угла поворота. У нас 3 координаты и соответственно 3 квантовых числа, в отличие от черного ящика, где оно одно. Поэтому мы сразу пишем 3 квантовых числа (главное, орбитальное и магнитное)

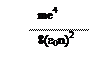E_nlm = E_п = -

- очень похоже на случай ящика.

Аналогично, в любом атоме существуют дискретные уровни энергии. Если атом многоэлектронный, задача усложняется тем, что там надо учитывать не только ядра, но и поле всех электронов, но решение будет очень похоже на это.

Электронные состояния молекул

Простейшая молекула, состоящая из двух атомов. Каждый атом имеет электронные состояния, поэтому и молекула тоже имеет. 2 ядра могут колебаться друг относительно друга – это будет колебательная составляющая спектра. Также молекула может крутится – это будет вращательная составляющая спектра.

Спектр молекулы будет гораздо богаче, и здесь не отдельные линии, а полосы.

Соотношение между колебательной и вращательной энергией

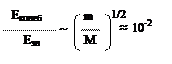
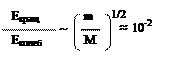
m – масса электрона, M –масса ядра.

Когда электрон переходит из одного состояния в другое, он может излучать или поглощать квант света (когда он идет вверх он поглощает, вниз – излучает). Не все переходы разрешены. Т.е. есть разрешенные, есть запрещенные переходы.

Твердое тело.

Нам нужно найти какую-то модель, по возможности упрощенную, чтобы примерно объяснить, как движется электрон в твердом теле.

Модель электронного газа.

Рассмотрим металл. Известно, что металл состоит из ионной решетки, и по одному электрону от каждого атома участвуют в процессе проводимости. Ионы кристаллической решетки очень маленькие, по отношению к кристаллу они занимают мизерную часть. Поэтому можно представить в качестве аналогии для описания твердого тела, что это трехмерный ящик.

Частица в трехмерном ящике.

Импульс в одномерном ящике p₀ = pħn/L, где L – это размер одномерного ящика. Здесь три степени свободы. По каждой степени свободы будет квантование. Поэтому появятся квантовые числа n_x = Lp_n/pħ n_y = Lp_n/pħ n_z = Lp_n/pħ. Ящик конечный. Для квадрата импульса получим такое выражение: p² = p²ħ²(n_x² + n_y² + n_z²)/L². В бесконечном ящике число энергетических состояний было бесконечно. Ящик конечный, но из него электрону не выбраться. Значит у него и число уровней конечно. Чем больше ящик, тем ближе расположены уровни, т.е. чем больше мы возьмем кусок этого металла, тем чаще эти уровни будут расположены. Может так оказаться, что число электронов значительно меньше, чем этих уровней. У электрона есть спин. В каждом состоянии не может быть больше одного электрона. В принципе они могут иметь одинаковую энергию, но обязательно у них должны быть противоположны спины. В целом электроны займут не все энергетические уровни. Уровень Ферми – уровень, до которого возможные состояния заняты электронами.

Найдем количество энергетических уровней, занятых электронами.

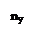
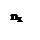
Гипотетическая система координат, по которой отложены квантовые числа. Какова величина максимального импульса? Он соответствует уровню Ферми. Сколько таких состояний, что p²ħ²(n_x² + n_y² + n_z²)/L² ≤ p_F²? Причем n_x,y,z ≤ p_FL/pħ – каждое квантовое число меньше максимального. Сколько всего этих квантовых чисел, т.е. уровней энергии? Столько, сколько всего точек с координатами n_x ≥ 0, n_y ≥ 0, n_z ≥ 0. Количество квантовых чисел равно 1/8 объема шара в пространстве квантовых чисел. Количество состояний:

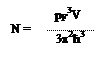
Максимальное значение – радиус шара. Количество энергетических уровней в единице объема:

Мы получили количество энергетических состояний, выраженное через максимальный импульс, который имеет частица. Импульс мы можем связать с энергией.

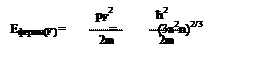Замечание: если состояние существует, не обязательно оно занято каким-то электроном. Но нам важно знать, сколько электронов в металле или полупроводнике. Мы должны уметь определять количество электронов потому, что количество электронов у нас фактически определяет проводимость твердого тела. Нам надо знать, сколько есть электронов с определенной энергией. Нам надо знать есть ли уровень, как много уровней с такой энергией вакантно и сколько электронов. Для того чтобы узнать количество электронов, нужно знать вероятность того, что данный уровень будет заполнен электронами. Концентрация электронов с данной энергией n(E)= S(E)f(E), S(E) – концентрация уровней с данной энергией, f(E) – вероятность заполнения этих уровней. Выражаем S(E):

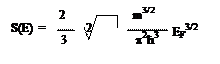Дифференцируем по энергии:

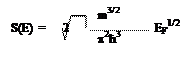
Мы получили, таким образом, плотность уровней, в зависимости от их энергии. Теперь, если мы знаем вероятность заполнения этих уровней, то тогда мы можем находить концентрацию электронов в каком-то конкретном случае. Функция вероятности заполнения уровня получается в статистической физике.

Распределение Ферми.

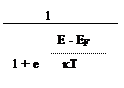f_F(E) =

k T= 0,025 эВ

Вероятность заполнения уровня Ферми = 0,5.

До уровня Ферми все уровни заполнены, а после уровня Ферми вероятность заполнения стремиться к 0. Чем выше температура, тем более размытой граница становится, а в близи абсолютного нуля это будет почти ступень. Распределение Ферми подходит для описания статистики электронов в любом твердом теле.

Рассмотрим, чем различаются проводники, диэлектрики, металлы.

Типы химической связи в твердых телах:

Для металлов это ионная решетка

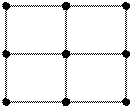
В узлах положительные ионы. В среднем один электрон проводимости на один ион. Электроны никак не связаны со своим ионом. Они свободно гуляют по всему металлу.

- металлическая химическая связь.

Для металла удельное сопротивление r < 10^-7 Ом∙м

Ковалентная связь. Это полупроводники (Si, Gr, Ga, As)

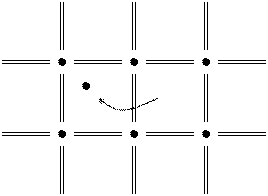
На внешней оболочке 4 электрона. Проводимость в чистом полупроводнике довольно низкая. Почти все электроны связаны. В принципе может какая-то связь разрываться, что влечет появление свободного электрона, которые тоже будут проводить ток. Удельное сопротивление полупроводника может меняться в очень широких пределах: 10^-5 < r < 10⁵ Ом∙м - зависит от того, есть ли там примеси или это чистый полупроводник. Верхняя граница условная – может быть и больше. Когда полупроводник с примесями его проводимость близка к проводимости металла. Когда связь разрывается, появляется электрон проводимости и появляется положительно заряженный ион – так называемая дырка. Это место может занять другой электрон. Соответственно отсюда дырка исчезнет, но там, откуда ушел этот электрон, дырка появится. 2 типа проводимости – электронная и дырочная.

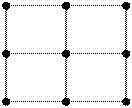Ионный тип проводимости:

Самый характерный пример – NaCl – поваренная соль. Это очень сильно полярная связь, и в результате образуется очень прочная кристаллическая решетка. Электроны притянуты в сторону одного элемента, а, значит, электронной проводимости нет. При такой связи материал является диэлектриком. Удельное сопротивление в полупроводнике > 10 –12 Ом*м.

Для того, что бы описать свойства твердых тел, такой простой аналогией как кристаллическая решетка не обойдешься. Невозможно ни в каком приближении попробовать решить уравнение Шредингера для такой системы из огромного количества ионов и электронов. Кристаллическая решетка естественно имеет периодическую структуру.

Дата добавления: 2014-01-06