Алгоритмы обучающихся самоорганизующихся карт

Лекция 13

Алгоритмы СОК основывается на соревновательном обучении без учителя. При этом обеспечивается сохраняющее топологию отображение из пространства большой размерности в элементы карты.

Обучается сеть Кохонена методом последовательных приближений, сначала нормализуются входные векторы 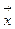и производится активация нейросети. Нормализация векторов может производиться следующими способами:

Переопределение компонентов вектора по формуле

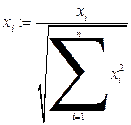; (1)

где знак:= это знак присваивания.

Увеличением размерности пространства на одну координату с выбором значения (n+1)-го компонента вектора, удовлетворяющего условие нормировки

; (2)

Для выполнения условия нормировки (2) предварительно нужно провести масштабирование компонентов вектора .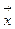

Нормализация входных векторов необходима при не большой размерности пространства, например n=2, n=3. ………………

При больших объёмах нейронной сети n>200, нормализация перестаёт оказывать влияние на процесс самоорганизации.

Алгоритм ответственный за построение СОК начинается с инициализации синоптических весов нейросети. Обычно синоптическим весам присваиваются небольшие значения, сформированные генератором случайных чисел. Когда процесс начинается с рандоминизированных (случайных) значение синоптических весов, выходные нейроны медленно выравниваются, поскольку при предъявлении входного образа на него реагирует не только отдельный нейрон, но также и его окрестность.

В этой ситуации важен выбор метрики, для измерения расстояния. В качестве меры расстояния используются следующие метрики:

1) 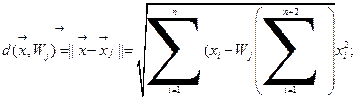(3)

(только первая сумма под корнем, просто не получается сделать)

(4)

2)Мера исп-я скалярное произведение.

(5)

Мера относительная формулы L1 (расстояние городских кварталов, или Манхэтонское расстояние)

(6)

(всё под корнем)

Мера относительности

; (7)

В процессе обучения размер окрестности вокруг нейрона победителя постепенно уменьшается. Сначала одновременно корректируются веса многих нейронов в окрестности нейрона победителя.

В процессе обучения на входные сигналы реагирует всё меньшее число нейронов. В конце обучения уточняются только веса связей нейрона победителя, они сдвигаются в направлении входного вектора с помощью множителя определяемого темпом обучения (Норма обучения 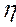). В процессе обучения уменьшается темп обучения.

В некоторых приложениях темп обучения снижается по мере уменьшения расстояния от нейрона победителя. Таким образом, в результате итеративной процедуры обучения, сеть организуется так, что элементы соответствующие центрам расположенным близко друг от друга в пространстве входов, будут располагаться близко друг от друга и на топологической карте. Алгоритм обучения нейросети с самоорганизацией, в которых на каждой итерации может обучаться только один нейрон, называется WTA (победитель забирает всё).

Архитектура нейронной сети в которой реализуется этот алгоритм имеет вид:

Широко употребляется WTM (победитель получает большее).

В последних алгоритмах, кроме нейрона победителя уточнаяют значение своих весов и нейроны из его ближайшего окружения. В этом случае чем дальше какой либо нейрон находится от нейрона победителя, тем меньше изменяются его синоптические веса.

Процесс корректировки весов для всех нерйронов j, который расположены в окресности нейрона победителя i, определяется обобщённой зависимостью:

(8)

где 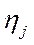(этто) – коэффициент обучения нейрона j, 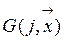– функция соседства. Имеется много вариантов алгоритма WTM которые отличаются, прежде всего, функцией соседства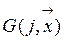

Дата добавления: 2014-01-06