Аттракторы

Обозначим функцию активации нейрона где V- взвешенная сумма его возбуждений.

Тогда состояние нейрона определяется выходным сигналом:

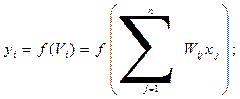
Учитывая, что при обратной связи «один ко многим» возбуждающими импульсами для нейрона являются выходные сигналы других нейронов, изменение его состояния описывается системой нелинейных дифференциальных уравнений.

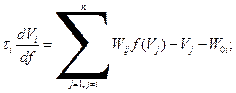(6)

для i =1,2,….,n.

здесь 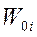пороговое значение заданное внешним источником

(тау) - это числовая константа. Она аналогична постоянной времени в уравнениях, описывающих динамические состояния.

В результате решения системы 6, что состояние нейрона будет равно:

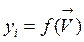; (7)

при определённом уровне возбуждения нейрона, который описывается значениями их выходных сигналов 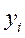, рекуррентной нерйонной сети, можно сопоставить энергетическую функцию Лякунова:

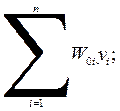(8)

эта функция связана с каждым возбуждённым состояние нейронной сети и убывает с течение времени.

Изменение состояния какого-либо нейрона приводит к изменению энергетического состояния всей нейросети в направлении минимума её энергии, в плоть до его достижения. Каждая из состояний системы сформированных на этапах обучения нейросети – это локальный минимум.

Обычно существует множество локальных минимумов.

В пространстве состояний локальные энергетические минимумы, представляются точками стабильности, которые называются Аттракторами.

Аттракторы – это множество, которое имеет размерность, меньшую размерности пространства состояния.

Лекция 15

здесь подмножеством понимается некоторая к-мерная поверхность, которая содержится в n-мерном пространстве состояний и которая описывается системой уравнений:

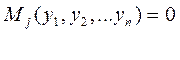; (1) j=1,2,..k; k<n.

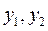… это элементы n-мерного вектора состояния системы

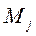– некоторая функция этих элементов

Аттракторы является ограниченными подмножествами.

К ним сходятся области начальных состояний пространства состояний не нулевого объёма с течением времени t.

Множество аттракторов может состоять из одной точки в пространстве состояний, в данном случае имеем точечный аттрактор. Множество аттракторов также может быть в форме периодической орбиты, в этом случае имеем устойчивый предельный цикл.

Под устойчивостью, здесь понимается асимптотическая сходимость к этому циклу близь лежащих траекторий.

Каждый из аттракторов окружён собственной чётко очерченной областью, которая называется бассейном (Областью аттракции)

Граница отделяющая один бассейн аттракции от другого наз-ся сепаротрисей.

На рисунке 1 граница бассейна аттракции состоит из траекторий T1 и T2 и Седловой точки Q (в трёх мерном пространстве похожа на седло).

Каждое начальное состояние системы находится в бассейне какого-либо аттрактора.

Аттракторы – это единственные равновесные состояния динамической системы, которые можно наблюдать экспериментально. Однако в контексте аттракторов равновесное состояния не обязательно яв-ся статическим или устойчивым, например придельный цикл.

Он представляет собой устойчивое состояние аттрактора, которое непрерывно изменяется во времени.

Нелинейные динамические системы, с порядком выше второго (порядок уравнения определяется порядком производной), характеризуются ещё одним классом нерегулярных аттракторов, которые наз-ся странными аттракторами.

Странные аттракторы имеют очень сложное поведение.

Они особенно интересны тем, что рассматриваемая система яв-ся детерминированной, то есть руководствуется фиксированными правилами.

В тоже время при наличии только нескольких степеней свободы поведение системы на столько сложно, что внешне, кажется, что это поведение носит чисто случайный характер.

В нелинейной динамической системе, когда орбиты аттракторов в окрестности начальных состояний стремятся отдалиться с течением времени, говорится о наличии странных аттракторов, а сама системы называется хаотической.

Другими словами, именно фундаментальные свойства чувствительности к начальным состояниям, делает эти аттракторы странными.

Чувствительсть означает следующее:

Если 2 идентичные системы начинают своё движение из начальных состояний

x(->) и x(->) + эпсилон (вектор)

где эпсилон – это очень малая велечина.

то их динамические состояния будут расходиться друг от друга. При этом расстояние между ними будет увеличиваться в среднем экспоненциально.

определение аттракторов для вычислительных объектов, например ассоциативной памяти, это одна из основных парадигм нейронных сетей. В данном случае необходимо управлять местом размещения аттракторов в пространстве состояния системы.

Алгоритм обучения будет в форме нелинейного динамического уравнения, которое управляет расположением аттракторов для кодирования информации в желаемом виде, либо обучение рассматриваемых временных структур.

Дата добавления: 2014-01-06