Система допусков на угловые размеры

ПОСАДКИ КОНИЧЕСКИХ СОЕДИНЕНИЙ

Принято угловые размеры разделять:

- на углы в плоскости, образованные двумя лучами, выходящими из одной точки;

- двугранные углы, образованные двумя плоскостями, исходящими из одной прямой (ребра). Однако для удобства измерений требования к точности относятся к углу в плоскости, т.е. углу, полученному пересечением двугранного угла плоскостью, перпендикулярной ребру;

- углы конусов составляют особую наиболее распространенную группу.

Все нормальные углы, применяемые при конструировании, можно разделить на три группы:

· нормальные углы общего назначения - наиболее распространенная группа, к которой относятся нормальные углы в плоскости, углы конусов и уклонов нормальных конусностей, углы призматических элементов (рис.64, б);

· нормальные углы специального назначения - ограниченно применяются в стандартизованных специальных деталях; к ним относятся углы и уклоны конусностей специального назначения;

· специальные углы - к ним относятся, во-первых, углы, размеры которых связаны расчетными зависимостями с другими принятыми размерами, и которые нельзя округлить до нормальных углов; во-вторых, углы, определяемые специфическими эксплуатационными или технологическими требованиями.

Углы конусов могут задаваться величиной угла, конусностью, обозначаемой буквой C, или уклоном i. Конусность и уклон связаны с основными размерами конуса.

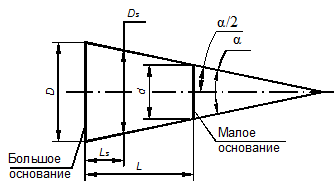
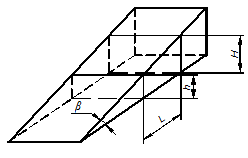
а) б)

Рис. 64. Основные размеры: а – конуса; б – призматического элемента

Прямая круговая коническая поверхность (в дальнейшем коническая поверхность или просто конус) - поверхность вращения, полученная прямой образующей, вращающейся относительно оси и пересекающей ее.

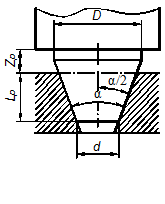
К основным размерам конуса относятся (рис.64, а): диаметр большого основания D, диаметр малого основания d, угол конуса α (конструкторская форма), угол уклона α /2, длина конуса L.

Под основанием конуса понимают окружности, образованные пересечением конической поверхности с перпендикулярными плоскостями, ограничивающими его в осевом направлении.

При рассмотрении допусков и посадок конических соединений пользуются терминами (рис.65), указанными далее.

Основная плоскость - плоскость поперечного сечения конуса, в котором задается номинальный диаметр конуса.

Базовая плоскость - плоскость, перпендикулярная оси конуса и служащая для определения осевого положения основной плоскости или осевого положения данного конуса относительно сопрягаемого с ним конуса.

В качестве базовой выбирают торцовую плоскость какого-либо заплечика, буртика или места перехода конуса в цилиндр, чаще всего со стороны большого диаметра. Базовая и основная плоскости конуса могут совпадать.

Базорасстояние конуса z_e или z_i - это расстояние между основной и базовой плоскостями конуса. Базорасстояние наружного конуса обозначается z_e, базорасстояние внутреннего конуса - z_i.

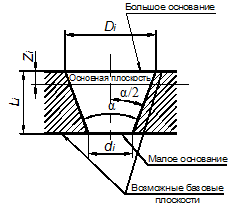
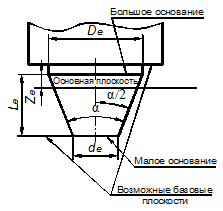
а) б) в)

Рис. 65. Основные параметры: а – внутреннего конуса; б – наружного конуса;

в – конусного соединения

Конусность С - отношение разности диаметров двух поперечных сечений к расстоянию между ними.

Конусность С в соответствии с определением рассчитывается по формуле: С = (D - d) / L = 2tg.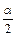

Конусность часто указывают в виде отношения 1: x, где x – расстояние между поперечными сечениями конуса, разность диаметров которых равна 1 мм, например C = 1:20.

Угол уклона (уклон) связан с размерами D, d, L соотношением:

i = C /2 = tg.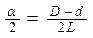

Для достижения взаимозаменяемости установлены ряды нормальных конусностей (ГОСТ 8593). Предусмотрены конусности специального применения для инструментальных конусов: конусы Морзе 0,1,2,3,4,5,6; конусы Морзе укороченные – В 7, В 10, В 12, В 16, В 18, В 22, В 24, В 32, В 45; конусы метрические.

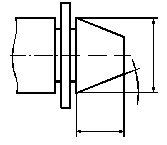
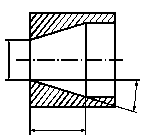
При измерении размеров универсальными средствами на конусные поверхности рекомендуется проставлять размеры, указанные на рис.66.

За единицу измерения плоского угла в международной системе единиц (СИ) принят радиан - угол между двумя радиусами, вырезающими на окружности дугу, длина которой равна радиусу.

Однако более удобной для измерений является система единиц, основанная на градусной мере, в которой для отсчета угла используются градус, минута, секунда. Соотношение между градусом и радианом: 1 рад = 57⁰ 17^' 45".

Кроме того, угол может быть задан приращением размера в линейной мере на определенной длине, например, уклон призматического элемента.

а) б)

Рис. 66. Рекомендуемые для простановки размеры:

а – на наружный конус; б – на внутренний конус

Стандартом ГОСТ 8908 предусматривается три ряда предпочтительных значений углов, заданных в угловых единицах измерения и установлено семнадцать степеней точности, обозначаемых в порядке убывания точности: AT 1, AT 2, AT 3 ,…AT 17. Латинские буквы AT обозначают допуск угла – разность между наибольшим и наименьшим предельными (допустимыми углами). При переходе от одной степени к другой значение допуска изменяется по геометрической прогрессии со знаменателем φ=1,6.

Области применения реально достижимых степеней точности:

1-4 – резервные степени;

5 - для конических калибров – пробок;

6 - для конических калибров-втулок;

7, 8 – высокая точность (конусы инструментов, конические концы валов и осей для точно центрируемых деталей);

9 -12 – нормальная точность (центровые гнезда и центры, угловые пазы в направляющих и т.д.);

13-15 – пониженная точность;

16-17 – для свободных размеров.

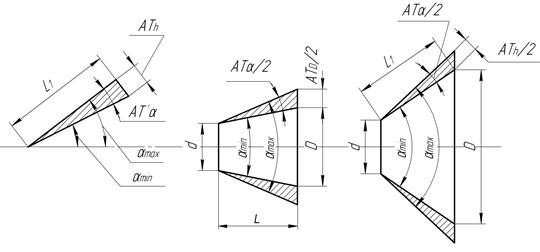
Стандартом для каждой степени точности установлены четыре вида допусков на угловые размеры (рис.67):

AT_α – допуск угла, выраженный в радианной мере (например, AT 17 = 80000 мкрад), и соответствующее ему точное значение в градусной мере (например, AT 17 = 4˚35΄ 01˝);

AT_α΄- допуск, выраженный в градусной мере, но с округленным значением по сравнению с выражением в радианной мере. Таким образом, угол 17 степени точности будет равен AT 17 = 4˚. На чертежах рекомендуется указывать округленный допуск угла;

AT_h – допуск, выраженный в линейной мере (в мкм) длиной отрезка на перпендикуляре к короткой стороне угла, противолежащего углу AT_α на расстоянии L₁ от вершины этого угла;

AT_D – допуск угла конуса, выраженный в линейной мере, как разность диаметров в двух нормальных к оси конуса сечениях плоскостями на заданном расстоянии между ними; определяется по перпендикуляру к оси конуса.

Исходными являются значения AT_α в микрорадианах; на их основе получены округленные значения допусков углов AT_α΄ в градусах, минутах, секундах, проставляемые на чертежах. Кроме того, те же допуски приведены в виде линейных величин AT_h (для призматических элементов) и AT_D (для конических поверхностей). Последние допуски используются при косвенном контроле угловых отклонений.

а) б) в)

Рис. 67. Виды допусков углов:

а - допуск угла; б – конусность С £ 1:3; в – конусность С > 1:3

Допуски углов назначают: для конусов с конусностью не более 1: 3 – в зависимости от длины конуса L; для конусов с конусностью свыше 1: 3 – в зависимости от длины образующей конуса L₁; для углов призматических элементов – в зависимости от длины меньшей стороны угла.

Таким образом, связь между допусками углов в угловых и линейных единицах определяется по формуле:

АТ_h = 10^-3 АT _a ∙ L,

где AT_h - в мкм; АТ _a – в мкрад; L – мм.

Для конусов с конусностью больше, чем 1: 3, значение АТ_D определяется по формуле:

АТ_D = АТ_h / cos(a/2),

где a – номинальный угол конуса. Для малых углов (С£1:3): АT_D @ AT_h.

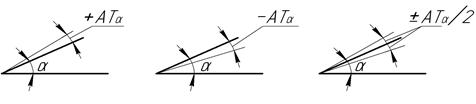
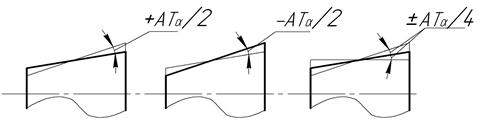
Применяются три основных типа расположения поля допуска относительно номинального угла: плюсовое (+ AT), минусовое (+ AT) и симметричное (± AT/2).

а) б) в)

Рис. 68. Типы расположения полей допусков для угла призматического элемента:

а - ( a + АТ _a); б – ( a – АТ _a); в – ( a ± АТ _a / 2)

а) б) в)

Рис. 69. Типы расположения полей допусков для угла конуса:

а - ( a + АТ _a); б – ( a – АТ _a); в – ( a ± АТ _a / 2)

При любом расположении поля допуска отклонения угловых размеров отсчитываются от номинального размера угла. Типы расположения полей допусков для угла призматического элемента представлены на рис. 68, а для угла конуса – на рис.69.

Дата добавления: 2014-01-06