Гидравлика 11 страница

7. ДИФФУЗИОННОЕ ПОДОБИЕ

Числа подобия для диффузионных процессов можно легко получить из уравнения диффузии вещества. Для одномерного движения уравнение молекулярной диффузии будет иметь вид

.

Подставим в уравнение выражения входящих в него величин через безразмерные и характерные значения (масштабы):

или .

Безразмерное число 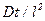называется диффузионным числом Фурье. Очевидно, что оно аналогично тепловому числу Фурье. При конвективном переносе вещества для одномерного движения воспользуемся уравнением

.

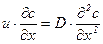Проделав аналогичные преобразования, получим

.

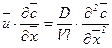Число называется диффузионным числом Пекле.

Число соответствует числу Re, определяющему структуру потока, и по тому, велико ли число по сравнению с единицей или мало, можно судить о том или ином характере режима переноса вещества. В первом случае молекулярной диффузией можно пренебречь по сравнению с конвективным переносом вещества, во втором - наоборот, молекулярная диффузия является определяющей.

Поделив число Ре на число Re, получим диффузионное число Прандтля 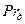, равное отношению кинематической вязкости к коэффициенту диффузии

.

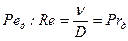Во многих работах число 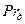называется числом Шмидта. Напишем теперь уравнение переноса вещества, отнесенное к разности концентраций на стенке и в окружающей среде

,

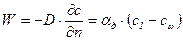где коэффициент переноса массы;

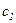концентрация в окружающей среде;

концентрация на стенке.

Запишем это уравнение в безразмерном виде

или

.

Тогда получим локальное число равное

.

Аналогично тепловому числу Nu можно, воспользовавшись средним коэффициентом переноса вещества 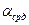, ввести среднее диффузионное число Нуссельта.

В газах числовое значение коэффициентов диффузии и вязкости имеет один порядок, поэтому .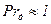

Иначе обстоит дело в жидкостях. Коэффициент кинематической вязкости подвижных жидкостей типа воды составляет около . Коэффициент диффузии молекул и ионов в водных растворах имеет порядок 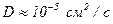, у макромолекул - 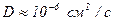. Поэтому в воде и сходных жидкостях будет . При возрастании вязкости коэффициент диффузии уменьшается по закону

,

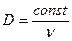поэтому число 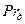растет с увеличением вязкости, пропорционально квадрату последней. В вязких жидкостях число 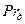достигает значения 10⁶ и более. Для жидких металлов число 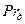значительно меньше единицы. Значения 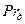для некоторых сред приведены в табл. X. 3.

Таблица X. 3

Диффунди-рующее вещество	Среда, в которой происходит диффузия	Температура °С	D м^2/с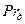
Hg	N2		3,25×10^-3	0,00424
СО2	Н2		6,05×10^-5	0,158
NН3	Воздух		2,17×10^-5	0,634
О2	N2		2,03×10^-5	0,681
НС1	Н2О		2,23×10^-6	0,81
С6Н6	Воздух		7,5×10^-6	1,83
С6Н6	Н2		2,94×10^-5	3,26

Следует отметить, что для газов тепловое и диффузионное числа Pr имеют одинаковый порядок, поэтому процессы переноса тепла и вещества в газах аналогичны, но процессы переноса тепла и вещества в жидкостях сильно отличаются друг от друга, так как сильно отличаются числа Pr и .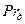

Можно заметить сходство между некоторыми числами подобия. Так, число Re похоже на числа Пекле тепловое и диффузионное. Исходя из этой аналогии, эти числа можно было бы назвать числами Рейнольдса - динамическим, тепловым и диффузионным, т.е.

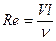; и .

Тогда в соответствии с ранее введенным определением имеем

и .

Эта аналогия используется и в электромагнитной гидродинамике (см. гл. XV), где вводятся магнитное и электрическое числа Рейнольдса.

10. ПЛОСКОЕ ТЕЧЕНИЕ МЕЖДУ ПЛАСТИНКАМИ

Приближенные методы решения для потоков при малых числах Re нами подробно не рассматриваются, поэтому в качестве примера приведем задачу о потоке между двумя очень близко расположенными пластинками.

Если обозначить малое расстояние между пластинками h и считать, что число 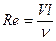очень мало, т.е. инерционные силы малы по сравнению с силами вязкости, то в уравнениях Навье - Стокса (X. 7.) можно пренебречь силами инерции и отбросить левую часть их. Тогда при отсутствии массовых сил система уравнений примет вид

; ; .

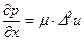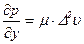Пусть уравнения плоскостей, между которыми течет жидкость, будут

и ,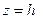

тогда, имея ввиду малость величины h, будем считать, что 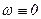и что изменение u и 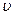по z будет сильнее, чем по х и у. Последнее означает, что

или ;

или ,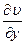

и соответственно

и и т. д.

Тогда, используя эти соотношения, получим уравнения (X. 17) в виде

; ; .

Так как из третьего уравнения видно, что давление не зависит от координаты z, то интегралы первого и второго уравнений будут

;

.

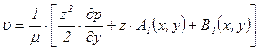Для нахождения А, В, А₁ и В₁ воспользуемся следующими граничными условиями: при z = 0 и z = h .

Учитывая эти условия, найдем u и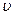

;

.

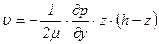Подставим найденные значения в уравнение неразрывности

,

получим

.

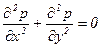Из равенства (X. 20) видно, что давление в рассматриваемом движении жидкости есть гармоническая функция.

Введем средние значения скоростей

; .

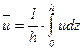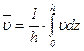Подставляя выражения (X. 19) в формулы (X. 21) и имея ввиду, что

,

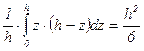получим

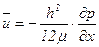
и

.

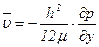Если теперь введем функцию

,

то она будет потенциалом средних скоростей, так как

и .

Тогда по равенству (X. 20) потенциал 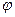будет удовлетворять уравнению Лапласа

.

Следовательно, средние скорости при движении вязкой жидкости с малым числом Re между двумя пластинами соответствуют скоростям потенциального потока. Последние соотношения используются для так называемой ламинарной аналогии потенциального потока (см. п. 2, гл. XVI).

9.1. Понятие о методе размерностей. Пи-теорема

9.2. Числа и критерии подобия

9.3. Методы моделирования

9.4. Методы аналогий

10. Общее уравнение энергии в интегральной и дифференциальной формах

11. Турбулентность и ее основные статистические характеристики

11.1. Осредненные параметры и пульсации

11.2. Стандарт пульсационной скорости и степень турбулентности

11.3. Двухслойная модель турбулентности

Дата добавления: 2014-01-06