Лекция №6

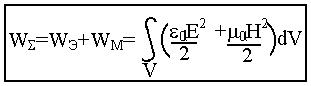Энергия электрического и магнитного поля связаны соотношением:

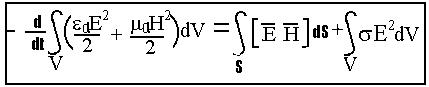Используя уравнения Максвелла, баланс энергий электрического и магнитного поля в течение некоторого времени в пределах некоторого объёма V, ограниченного поверхностью S, можно представить в виде уравнения Умова-Пойнтинга:

Левая часть уравнения характеризует расход энергии электромагнитного поля за единицу времени. Правая часть уравнения:

Ø Первое слагаемое представляет собой поток энергии в окружающее пространство через замкнутую поверхность S объёма V за отрезок времени t.

Ø Второе слагаемое выражает энергию в соответствии с законом Джоуля-Ленца, которая преобразуется в тепло внутри объёма V за единицу времени.

Таким образом, любое изменение энергии электромагнитного поля связано или с преобразованием этой энергии в тепло, или с излучением её в окружающее пространство.

Векторное произведение векторов напряжённости электрического и магнитного полей обозначают через вектор ПОЙНТИНГА:

Направление действия вектора Пойнтинга связано с векторами напряжённости электрического и магнитного полей правилом буравчика: Если плоскость движения ручки буравчика совместить с плоскостью действия векторов напряжённости электрического и магнитного полей, то вращение ручки буравчика по кратчайшей линии от вектора напряжённости электрического поля к вектору напряжённости магнитного поля по часовой стрелке укажет направление действия вектора Пойнтинга.

Вектор Пойнтинга определяет количество энергии, распространяющейся в единицу времени через единичную площадку, перпендикулярную направлению потока энергии. Таким образом, излучаемая из объёма энергия или поступающая в объём через ограниченную поверхность энергия согласно теореме Умова-Пойнтинга количественно равна интегралу от скалярного произведения Вектора Пойнтинга на бесконечно малый элемент dS.

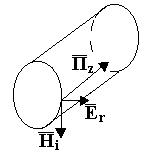Энергия, которая распространяется вдоль НС Э, характеризуется составляющими Er и Hi.

Таким образом, для определения количества энергии, переданной по НСЭ, достаточно знать две составляющих поля Er и Hi, причём данное соотношение характеризует идеальную цепь, когда вся энергия передаётся по НСЭ без преобразования в тепло. В реальных цепях с потерями, обладающих активным сопротивлением, часть энергии согласно закону Джоуля-Ленца будет теряться, преобразовываясь в тепло. Соответственно НСЭ, обладающие меньшим сопротивлением, являются более качественными. С учётом применения для НСЭ цилиндрической системы координат интеграл, характеризующий количество энергии, удобнее записывать в этой системе координат.

Рассмотрим варианты распространения энергии поля по НСЭ:

Ø

Процесс передачи энергии:

Ø Процесс излучения энергии:

Ø Процесс поглощения энергии:

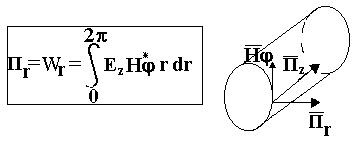Согласно закону Джоуля-Ленца:

W_п=I²Z

Z=R+iWL

Таким образом, теорема Умова-Пойтинга напрямую выводит на аналитические выражения для параметров передачи цепи R и L.

Дата добавления: 2014-01-06