Лекция №9

Конструктивные особенности коаксиальных пар позволяют передавать широкий спектр частот и обеспечивают высокую помехозащищённость. Это связано с закрытостью данной системы электросвязи от взаимных и внешних полей. Рассмотрим это на примере магнитного поля:

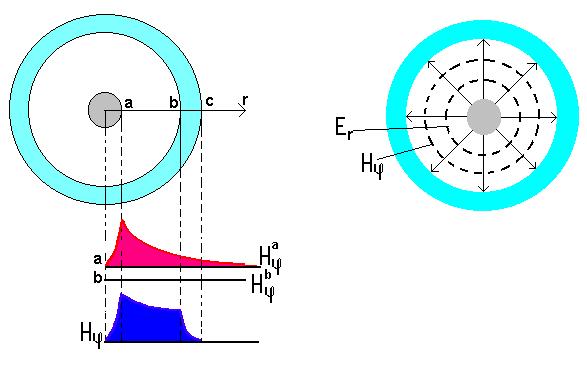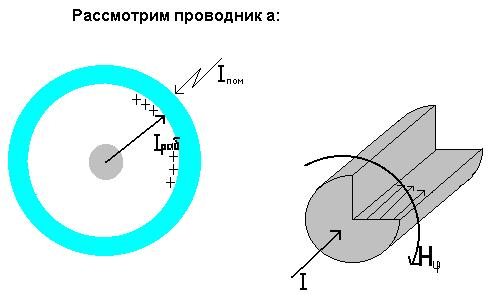Поверхностный эффект является причиной активного сопротивления с ростом частоты.

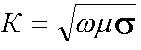Количественной характеристикой действия вихревых токов является коэффициент вихревых токов:

Все частотно-зависимые параметры проводников цепи зависят только от вихревых токов.

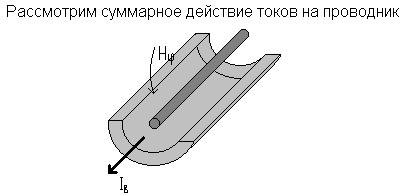Вывод: чем выше частота, тем больше рабочий ток смещается на внутреннюю поверхность внешнего проводника, и тем выше защищённость коаксиальной пары от внешних электромагнитных помех. Таким образом, мы видим, что в симметричных цепях, помехозащищённость ухудшается с ростом частоты. А в коаксиальных цепях с ростом частоты помехозащищённость, напротив, увеличивается.

Рассмотрим процессы в коаксиальной паре без учёта действия вихревых токов, а значит и без учёта потерь в проводниках. Согласно уравнению Умова-Пойнтинга передача энергии в такой цепи будет соответствовать направлению вектора Умова-Пойнтинга вдоль оси Z:

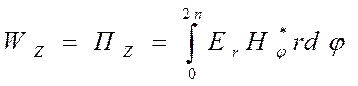Для определения величины энергии необходимо найти составляющие Е_r и Н_j.

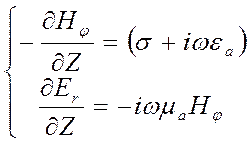Рассмотрим систему уравнений Максвелла для этих составляющих:

Предполагаем, что электромагнитное поле изменяется по экспоненциальному закону и составляющие Е_r и Н_j можно записать в следующем виде:

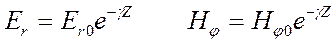Где g-коэффициент распространения цепи, Е_r0 и Н_j0-начальные значения составляющих поля. Беря от этих значений первые производные по координате z, получим:

Подставим значения производных в исходные уравнения и получим:

Разделим первое уравнение на второе:

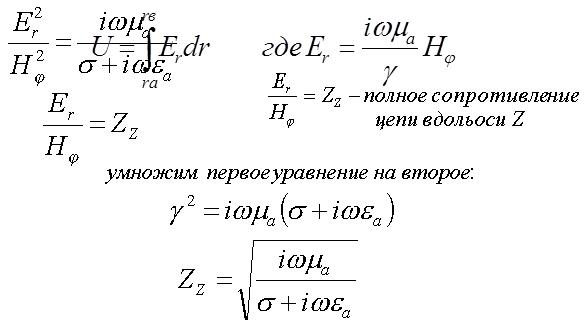Величина напряжения, действующего между проводниками цепи, может быть определена из интеграла:

Преобразуем выражение Е_r:

Из уравнения однородной линии известно соотношение:

Выводы: в идеальной цепи активное сопротивление равно нулю, индуктивность не зависит от частоты и определяется только межпроводниковой внешней индуктивностью. Проводимость изоляции существенно зависит от проводимости среды. Ёмкость зависит от диэлектрической проницаемости среды.

В реальной цепи всегда действуют вихревые токи. С учётом этого уравнение Умова-Пойнтинга и направление действия векторов будет:

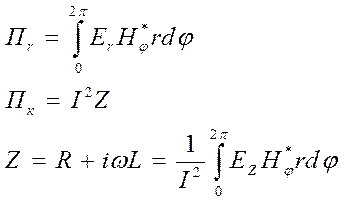Найдём Е_Z и Н_j.

Полное сопротивление цепи с потерями будет складываться из Z_a и Z_в.

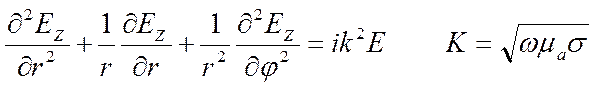Рассмотрим систему уравнений Максвелла для Е_Z и Н_j, которые путём преобразований можно представить в виде волновых уравнений второго порядка.

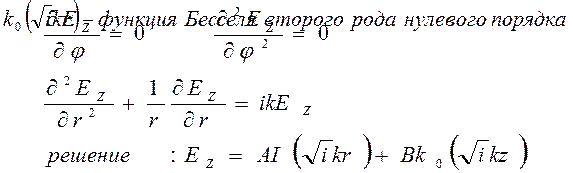Здесь А и В - постоянные интегрирования, I₀ – Функция Бесселя первого рода нулевого порядка.

Данные функции Бесселя определяют изменение параметров передачи в зависимости от действия вихревых токов. В аргумент этих токов непосредственно входит коэффициент вихревых токов коэффициента радиуса проводника r.

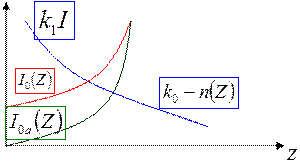
Графики функций Бесселя:

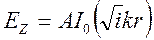Рассматривая электрические процессы в проводниках, мы выясним, что с увеличением радиуса и, соответственно, координаты r величина напряжённости поля возрастает от центра к поверхности проводника, то есть поведение функции Бесселя второго рода нулевого порядка не соответствует физическому смыслу явления. Поэтому величиной k₀ пренебрегаем и решение для составляющей E_Z будет иметь вид:

Из системы уравнений Максвелла можно записать выражение для Н_j:

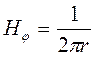Но с другой стороны:

Приравнивая координату r к радиусу внутреннего проводника, находим постоянную интегрирования А:

Подставим в решение постоянную интегрирования А:

если f>60кГц, то:

Для медного проводника выражение можно упростить:

Рассмотрим решение волнового уравнения Гельмгольца:

Подставляя Е_r и Нj в исходные уравнения, Умова-Пойтинга, получим выражение для внешнего проводника цепи:

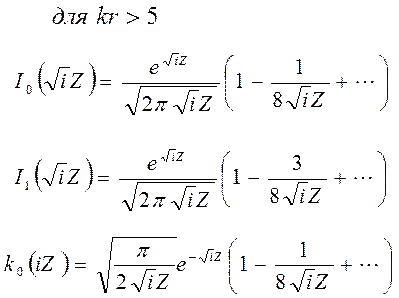Функции Бесселя можно представить в виде асимптотически сходящихся рядов следующего вида:

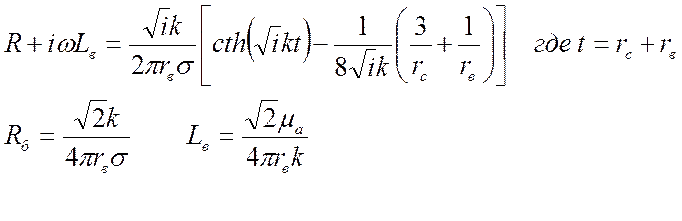Ограничивая эти ряды тремя составляющими, и, подставляя их значения в сопротивление проводника, получим:

Для медных проводников:

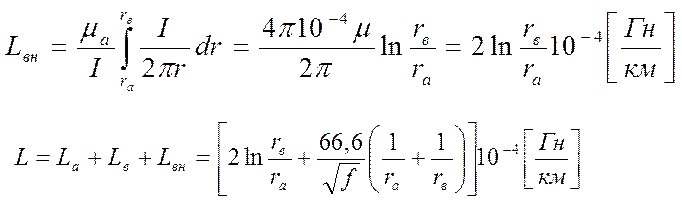
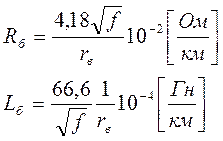Наряду с внутренней индуктивностью проводников в коаксиальной цепи действует межпроводниковая индуктивность.

Если внешний проводник сделан из алюминия, то:

Дата добавления: 2014-01-06