Расчёт прочности зубьев по контактным напряжениям

Расчёт цилиндрических прямозубых передач на прочность

Расчёт цилиндрических зубчатых передач на прочность стандартизован ГОСТ 21354-75.

ГОСТом предусмотрен расчёт прочности зубьев по контактным напряжениям и расчёт прочности по напряжениям изгиба.

Так как усталостное выкрашивание, вызываемое действием переменных контактных напряжений является основным видом повреждения зубьев в закрытых передачах, то расчёт по контактным напряжениям является основным (проектным) расчётом для закрытых передач.

Установлено, что наименьшей контактной выносливостью обладает околополюсная зона рабочей поверхности зубьев. Поэтому расчёт напряжений принято выполнять при контакте в полюсе зацепления.

Контакт зубьев можно рассматривать как контакт двух цилиндров с радиусам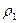и и сжимаемых силой F_n (рис.3.4).

При этом контактные напряжения определяются по формуле Герца:

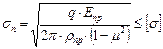(3.6)

где 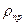- приведённый радиус кривизны.

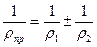(3.7)

+ - при внешнем зацеплении;

- -при внутреннем зацеплении.

С учетом параметров зубчатого зацепления 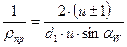(3.8)

q - удельная нагрузка на единицу длины контактной линии зуба.

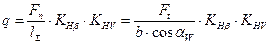(3.9)

где 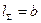- ширина зубчатого венца для однопарного зацепления.

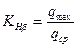- коэффициент неравномерности нагрузки по ширине колеса при расчёте по контактным напряжениям. Величина 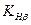определяется по специальным графикам в зависимости от схемы передачи и материала зубьев.

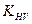- коэффициент динамической нагрузки учитывает дополнительные динамические нагрузки, вызванные погрешностями изготовления передачи.

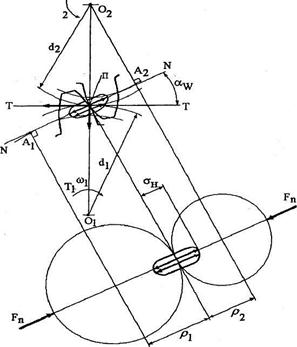Рис.3.4

Введем обозначение:

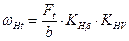(3.10)

Тогда формулу (3.9) запишется следующим образом:

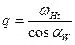(3.11)

При расчёте на контактную прочность всем величинам приписывают индекс «Н».

Подставив теперь в формулу Герца (3.6) значения 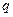(3.11) и 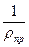(3.8) получим:

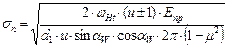(3.12)

Учитывая что 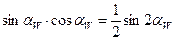, получим:

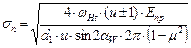(3.13)

Введем обозначения:

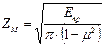- коэффициент, учитывающий свойства материала зубчатых колес,

где: E_пр - приведенный модуль упругости. Для стальных зубчатых колес 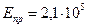МПа

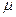- коэффициент Пуассона. Для стальных зубчатых колес . Тогда .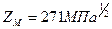

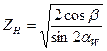- коэффициент, учитывающий форму сопряженных поверхностей,

где 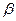- угол наклона зубьев. Для прямозубого колеса , .

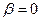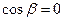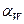- угол зацепления. Для зубчатых колес нарезанных без смещения 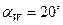. Тогда .

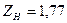Окончательно получим

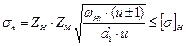(3.14)

Величина расчётных контактных напряжений одинакова для шестерни и колеса. Поэтому расчёт выполняют для того колеса, у которого допускаемые напряжения меньше. Последняя формула (3.14) удобна, когда размеры передачи известны.

Для проектного расчёта окончательную формулу решают относительно какого-либо размера передачи (обычно 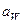или 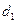). Так как неизвестных размеров несколько, то остальные размеры выражают через искомый и задают на основе опыта.

В нашем случае обозначим: 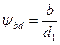- коэффициент ширины шестерни относительно ее диаметра.

Найдём

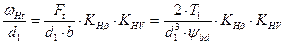(3.15)

Подставив выражение (3.15) в формулу (3.14) для расчета контактных напряжений, получим:

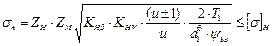(3.16)

Решая уравнение (3.16) относительно 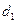, находим

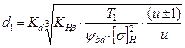, (3.17)

где .

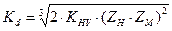Значение 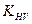обычно невелико и при предварительных расчётах принимают 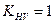, тогда .

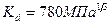Выразим крутящий момент 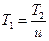, диаметр делительной окружности .

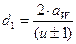Введем коэффициент ширины колеса относительно межосевого расстояния .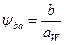

После ряда преобразований получим:

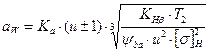, (3.18)

где .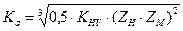

При 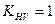для стальных прямозубых колёс .

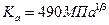Дата добавления: 2014-01-06