Движение тела по окружности

Закон. Все движения происходят одинаково в покоящихся системах отсчета, или движущихся относительно друг друга с постоянной скоростью. Это принцип одинаковости или равнозначности инерциальных систем отсчета или принцип независимости Галилея.

Общие законы движения

1 Закон. Если на тело не действуют другие тела, оно сохраняет состояние покоя или равномерного прямолинейного движения. Это закон инерции, первый закон Ньютона.

3 Закон. Все движения материального тела происходят независимо друг от друга и складываются как векторные величины. Так любое тело на земле одновременно участвует в движении Солнца с планетами вокруг Центра Галактики со скоростью около 200 км./сек, в движении Земли по орбите со скоростью около 30 км/сек, во вращении Земли вокруг своей оси со скоростью до 400 м /сек и возможно в других движениях. Получается весьма замысловатая криволинейная траектория!

Если тело брошено с начальной скоростью Vo, под углом a к горизонту то дальность полета –S вычисляется по формуле:

S = 2 V*SIN(a) * COS(a) / g = V*SIN(2a) / g

Максимальная дальность при a =45 градусов. Максимальная высота полета –h вычисляется по формуле:

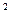h = V* SIN(a)/2g

Обе эти формулы можно получить, если учесть, что вертикальная составляющая Vo*SIN(a), а горизонтальная Vo * COS(a), V =g*t, t =V/g.

Cделаем подстановку в основную формулу для высоты

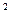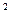h = g t/2 = g* (V/g)/2 = V/2g = V* SIN(a)/2g.

Это и есть нужная формула. Максимальная высота при бросании вертикально вверх, при этом

a =90 градусов, SIN(a) =1; h = V*/2g

Для вывода формулы дальности полета нужно горизонтальную составляющую умножить на удвоенное время падения с высоты h. Если учитывать сопротивление воздуха, то путь будет короче. Для снаряда, например, почти вдвое. Одной и той же дальности будут соответствовать два разных угла бросания.

Рис.11 Траектории полета тела брошенного под углом к горизонту. Рисунок справа движение по окружности.

w- Угловая скорость вращающегося тела; радиан / сек

b -Угловое положение вращающегося тела; радианы или градусы относительно оси. Радиан это угол под которым видна из центра окружности дуга равная радиусу окружности, соответственно рад=360/6,28 = 57,32 градусов

а-угловое ускорение измеряется в рад/сек²

b = bо + w * t, Угловое перемещение от bо.

S = b *R -Линейное преремещение по окружности радиуса R.

w =(b - bо)/(t –to); -Угловая скорость. V = w* R – Скорость по окружности

T = 2*p/w =2*p*R/V Отсюда V = 2*p*R/T

a =ao + w/t – Угловое ускорение. Угловое ускорение определяется тагенциальной силой и при ее отсутствии будет равномерное движение тела по окружности. При этом на тело действует центростремительное ускорение, которое в течение оборота изменяет скорость в 2*p раз. Его величина определиться формулой. a =DV/T =2*p*V/2*p*R/V =V/R

Средние величины скорости и ускорения не позволяют рассчитать положение тела при неравномерном движении. Для этого необходимо знать значения скорости и ускорения в короткие промежутки времени или мгновенные значения. Мгновенные значения определяются через производные или дифференциалы.

Дата добавления: 2014-01-06