Оператор цикла с параметром

End.

Repeat

Begin

Var

End.

Begin

Begin

Var

End.

Begin

End.

Begin

S:= 0; k:=1;

repeat S:= S + 1/sqr(k);

k:= k + 1;

until k > 20;

writeln(‘ S = ’, S:10:5):

Задачу примера 4.15 можно решить с помощью другого варианта циклического алгоритма.

1. Положить S = 0, k = 1.

2. Если k > 20, то СТОП, иначе продолжить.

3. Вычислить S + 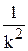и записать результат в S.

4. Увеличить k на 1.

5. Повторить шаг 2.

На PASCAL этот алгоритм удобно записать с помощью цикла while, т.к. в данном варианте проверка условия прекращения цикла происходит до выполнения действия.

var S: real;

k: integer;

S:= 0; k:=1;

while k <= 20 do

begin S:= S + 1/sqr(k);

k:= k + 1;

end;

writeln(‘ S = ’, S:10:5):

В приведенных примерах количество повторений тела цикла можно оценить еще до его выполнения. Однако, во многих задачах количество этих повторений заранее не известно и вычислено быть не может. Опера­торы repeat и while позволяют организовывать такие циклы. В сле­дующих двух примерах рассмотрим нахождение суммы бесконечного ря­да с заданной точностью.

Пример 4.16. Найти сумму членов бесконечно убывающей геометрической прогрессии с точностью до слагаемого, меньшего заданной величины e:

z = 1 + x + x ² + x ³ +…+ xⁿ + …

При нахождении суммы такого ряда не следует вычислять от­дельно каждый элемент. Достаточно установить зависимость, по ко­торой из предыдущего элемента образуется следующий. Обозначим через a_n = xⁿ – n-й член прогрессии, тогда

a_n+1 = x^{n +1} = a_n × x; a₀ = 1.

Та­кой подход позволяет сократить количество вычислительных операций и уменьшить время счета. Сумму будем накапливать в переменной S, которую предвари­тельно необходимо обнулить, как и в предыдущем примере.

Условие окончания цикла – |a_n | £ e., которое означает, что последнее слагаемое по модулю меньше e. Так как слагаемые данного выражения убывают, то и все следующие слагаемые малы, значит, сумма от последующих сложений практически не увеличится и процесс накопления суммы можно прекратить.

Ниже приведены два варианта программы. В первом варианте использован оператор while, во втором – repeat. В программах a_n обозначено именем а.

Первый вариант

x, s, eps, a: real;

write ('введите х и epsilon - ');

readln (x, eps);

s:=0;

a:=1; { задание параметру цикла его начального значения }

while abs(a) > eps do { проверка условия выхода из цикла }

s:= s + a; a:= a * x;

end;

writeln ('сумма прогрессии = ', s:10:3)

Второй вариант

x, s, eps, a: real;

write ('введите х и epsilon - ');

readln (x, eps);

s:= 0;

a:= 1; { задание параметру цикла его начального значения }

s:= s + a; a:= a * x;

until abs(a) < eps; { проверка условия выхода из цикла }

writeln ('сумма прогрессии = ', s:10:3)

Дата добавления: 2014-01-06