
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модели распространения вредных веществ в окружающей среде
|
|
|
|
Модели распространения вредных веществ в окружающей среде являются инструментом для количественной оценки техногенных воздействий.
Моделированию процессов распространения тех или иных субстанций в различных средах посвящено довольно большое количество фундаментальных работ. Вопросы, связанные с закономерностями турбулентной диффузии примесей в атмосфере и водных средах, нашли отражение в трудах отечественных и зарубежных ученых. Разработано достаточно большое количество математических моделей, которые могут использоваться для проведения расчетов.
Модели атмосферной диффузии классифицируются по многим признакам. В частности, с учетом масштаба турбулентных движений воздушных масс их принято подразделять на:
- модели локального масштаба, обеспечивающие наибольшую точность оценок на расстояниях до 10 км.
- мезомасштабные модели, которые рекомендуется использовать для расстояний от 10 до 200 км;
- модели регионального масштаба, рекомендуемые для расстояний от 200 до 1000 км;
- модели глобального масштаба, используемые при расстояниях свыше 1000 км.
В зависимости от характера источника аварийных выбросов, модели распространения опасных веществ делятся на модели "клуба", основывающиеся на предположении о мгновенно действующем источнике загрязнения, и модели "факела", в которых рассматривается постоянно действующий источник выбросов, точнее говоря, источник с конечным временем действия.
Существует классификация моделей по использованному при их разработке подходу к описанию турбулентной диффузии. По этому признаку выделяются статистические, полуэмпирические и комбинированные модели.
В основу моделей первого вида положено предположение о том, что процесс распространения примеси в атмосфере во всех направлениях имеет статистические характеристики состояния систем диффундирующих частиц. При статистическом подходе принимается гауссовский закон распределения диффундирующей примеси по координатным осям.
Статистическая модель для мгновенного точечного источника в общем случае может быть записана в виде [92] 
где С(х, у, z, t) — концентрация дифундированного вещества как функция пространственных координат и времени; Q — количество выброшенного вещества; и, v, w — средние значения скоростей ветра по направлениям х, у, z; с2,о2,02 — дисперсии примеси по направлениям х, у, z; f. f, f. — поправки на обеднение облака за счет радиоактивного распада или разложения вещества, его сухого осаждения и вымывания.
Следует заметить, что в соответствии с приведенной моделью процесс переноса "клуба" рассматривается в движущейся системе координат.
Статистическая модель факела, приемлемая для расстояний до 10-12 км, имеет вид:

где Q - скорость выброса вещества из постоянно действующего точечного источника: Н, — эффективная высота источника, определяемая с учетом подъема факела за счет термического и динамического всплытия струи. Остальные величины в прежних обозначениях.
Модель разработана в предположении, что скорость и направление ветра не изменяются с удалением от источника и с высотой. При расчетах для больших расстояний она дает заниженные оценки.
Подробное описание модели содержится в Руководстве по организации контроля состояния природной среды в районе расположения АЭС.
Полуэмпирическая модель для источника с конечным временем действия, учитывающая профиль ветра по высоте и изменение с высотой коэффициента турбулентной диффузии, по Берлянду [150] выражается формулой

где ^ - вертикальная составляющая коэффициента турбулентной диффузии на высоте 1м; ky - горизонтальная составляющая коэффициента турбулентной диффузии; п, т — безразмерные параметры из формул вертикальных профилей скорости ветра и вертикальной составляющей коэффициента диффузии:
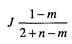
|
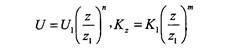
- функция Бесселя от мнимого аргумента.
Остальные величины в прежних обозначениях.
Комплексная модель атмосферной диффузии учитывает наличие подстилающей поверхности, обусловливающей определенные различия в характере турбулентной диффузии в горизонтальных и вертикальном направлениях. В модели принимается во внимание, что размеры вертикальных пульсаций ограничиваются подстилающей поверхностью, вследствие чего можно не учитывать рост масштаба вихрей по мере удаления от источника. В связи с этим модель в части, касающейся распространения примеси в вертикальном направлении, строится как полуэмпирическая, горизонтальное же распределение примеси описывается на основе статистических законов.
Соотношение, отражающее эти соображения, имеет вид:
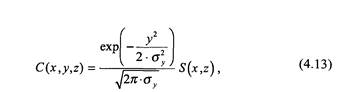
где S(x, z) — некая функция, описывающая закономерности изменения количества примеси, если условно предположить, что вся она сосредоточена в вертикальной плоскости х, z.
Заметим, что конкретное выражение для функции S(x, z) находится путем решения уравнения турбулентной диффузии применительно к условиям выброса и распространения примеси.
Модели, описывающие распространение примесей в атмосфере, различаются также по использованному при их разработке приему решения основного уравнения переноса и диффузии примеси

где К — вектор коэффициентов турбулентной диффузии; V — вектор поля скоростей в воздушной среде. Остальные величины в прежних обозначениях.
По указанному выше признаку выделяются следующие модели:
- модель типа "ящика";
- конечно-разностные модели;
- статистические регрессионные модели;
- модели, разработанные методом "Монте-Карло".
Описание этих моделей приводится в Руководстве. Поэтому ограничимся лишь некоторыми замечаниями по их сути.
Суть моделей типа "ящик" состоит в том, что атмосфера разбивается на ряд объемов или ящиков, для каждого из которых составляется уравнение материального баланса с учетом источников, стоков и переноса примеси из одного ящика в другой. Многоящичные модели являются конечно-разностным аналогом приведенного выше уравнения переноса и диффузии.
Конечно-разностные модели примыкают по своей сути к моделям ящичного типа. Эти модели основаны на численном решении уравнения (4.14) с теми или иными упрощениями и допущениями. При этом атмосфера аппроксимируется набором трехмерных расчетных ячеек. Схема аппроксимации может быть феменологической и конечно-разностной, характерной для уравнений параболического типа.
Статистические регрессионные модели строятся на основе статистических данных о загрязнениях и используются для краткосрочного прогноза.
Модели распространения вредных веществ в водных средах несколько сложней, чем модели атмосферной диффузии. Дело в том, что водная среда богаче различного рода процессами взаимодействия с вносимыми в нее примесями.
Основными процессами, определяющими распространение вредных веществ в поверхностных водах, являются:
- перенос с перемещающимися массами воды;
- турбулентная диффузия примесей;
- осаждение на дне водоема вредных веществ, находящихся в форме взвесей и коллоидных частиц;
- переход осадков, содержащих вредные вещества, вновь во взвешенное состояние;
- сорбция и десорбция вредных примесей различного рода неорганическими и органическими веществами;
- захват биотой;
- разложение и распад (в том числе и радиоактивный) вредных веществ и т.п.
С учетом этого основное уравнение дисперсии вредных (опасных) веществ в воде, движущим началом которой является совокупность процессов переноса и диффузии, имеет вид:
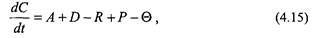
где С - концентрация вещества; А - изменение концентрации вещества, обусловленное его переносом с потоком водных масс, обычно называемом адвекцией; D - изменение концентрации вещества за счет диффузии; R — убыль вещества из водной среды за счет осаждения на взвесях с последующим отложением; Р — изменение концентрации за счет различного рода источников и стоков, седиментации, поглощения биотой (биологического захвата) и т.п.;
Q - убыль вещества за счет разложения и распада.
Заметим, что при описании атмосферной диффузии обычно процесс адвекции и диффузии рассматривается как единый процесс турбулентной диффузии. Для водной же среды в силу наличия совершенно определенных перемещений водных масс, обусловленных, например, речными течениями, удобнее два этих переноса вещества рассматривать отдельно, что и нашло отражение в приведенном выше уравнении. Вместе с тем для морской среды при математической формулировке задачи адвекция и диффузия учитываются в рамках единого явления - турбулентной диффузии.
В приведенном выше уравнении адвекция и диффузия и осаждение вредных веществ на взвесях описываются уравнениями:

где U, V, W — скорости перемещения водных масс по направлениям осей; х, у, z - составляющие коэффициента диффузии; 5 -концентрация взвешенных отложений; т - коэффициент равновесного распределения вещества между отложениями и водой.
Распространение загрязняющих примесей в воде под действием течений и турбулентной диффузии зависит от характера источников загрязнения. Обычно выделяют три масштаба распространения примесей в водной среде: локальный, мезо-масштабной и макромасштабный.
Локальный масштаб имеет место при источнике небольшого размера, с малым временем действия и расходом. В этом случае при проведении расчета источник принимается за точечный, примесь считается консервативной, а составляющие скорости течения постоянными. Для проведения расчетов распространения примесей могут применяться аналитические модели.
Мезомасштаб и макромасштаб распространения примесей реализуются при постоянно действующем мощном источнике загрязняющих веществ. При этих масштабах чаще всего применяются численные методы решения уравнения турбулентной диффузии и проведения расчетов.
Конкретные математические модели, необходимые для расчетов дисперсии примесей в реках, эстуариях, прибрежных и открытых зонах водных объектов, содержатся, например, в отчете ИБАЭ РАН по работе, связанной с разработкой методик и компьютерной реализацией базовых моделей распространения радионуклидов в гидрологической сети, в учебнике А. М. Владимирова по охране окружающей среды и других изданиях. Несмотря на наличие довольно большого числа разработок по моделированию дисперсии радиоактивных, других вредных веществ в водных средах, имеется объективная необходимость в систематизации этих моделей и выработке рекомендаций по их использованию в тех или иных ситуациях.
Модели миграции и дисперсии вредных веществ в грунтовых водах строятся с учетом вертикального переноса через неводонасыщенную область и дисперсии и переноса в водонасыщенных зонах. При моделировании подземной гидрологической дисперсии учитываются такие процессы, как сорбция-десорбция веществ в почвенных структурах, ионный обмен, разложение веществ биотой и т.п. Важное значение в связи с этим имеет исходная информации о составе почв и подземных потоках воды.
Для проведения расчетов приемлемыми являются модели, описывающие миграцию и перенос радионуклидов в подземных водах, которые рекомендованы комиссией по ядерному регулированию (NRC). Разработка этих моделей проводилась применительно к точечным, горизонтальным и вертикальным линейным и площадным источникам вредных веществ. Таким образом, при решении практических задач имеется возможность выбора подходящей для конкретных условий модели.
Как известно, одним из возможных путей нанесения ущерба для здоровья людей является попадание загрязнений внутрь организма при потреблении продуктов питания и воды.
Построение моделей пищевых цепочек, которые бы описывали распространение вредных веществ в компонентах окружающей среды, включая растения, животных, продукты питания, представляет довольно сложную задачу.
Адекватная структура пищевой цепи может быть определена на основе анализа рационов питания, возможных путей загрязнения продуктов, входящих в эти рационы.
Модели пищевых цепей обычно подразделяются на наземные и водные. Те и другие, как правило, основываются на рассмотрении переноса вредных веществ между "камерами", представляющими собой различные компоненты экосистем.
При этом принимаются во внимание все возможные биоаккумуляционные факторы, влияющие на каждую камеру.
На основе моделей дисперсии вредных веществ в различных средах и перемещения их по пищевым цепочкам возможно произвести оценку полей концентраций и дозовых нагрузок в районах расположения объектов и по пути распространения этих веществ, падающих на персонал, население, а также популяции животных и растений, биоценозы и экосистемы. Расчетные схемы определения уровней концентраций и дозовых нагрузок устанавливаются исходя из конкретных целей проводимой оценки и условий обстановки.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 2924; Нарушение авторских прав?; Мы поможем в написании вашей работы!