Статистика равновесных носителей заряда

В п/п есть определённая система энергетических уровней, которые в зависимости от условий могут быть заполнены электронами или свободны. Для определения концентрации подвижных электронов и дырок нужно знать:

1)количество квантовых состояний, в которых могут находиться носители;

2) какая часть из этих состояний заполнена электронами или дырками при заданных условиях.

1.Для изолированного электрона количество квантовых состояний определяется совокупностью 4-х квантовых чисел: 3 из них описывают волновую функцию электрона, а четвёртое описывает собственный момент кол-ва движения или спокойном. В системе электронов испытывающих электростатическое отталкивание, нельзя считать, что каждый электрон движется в постоянном электрическом поле, т.е. нельзя считать, что для каждых отдельных электронов??????? свои квантовые состояния. Следует рассматривать квантовые состояния системы в целом. Для вычисления равновесного распределения электронов по квантовым состояниям при различных температурах и по концентрации примесных атомов надо сначала вычислить распределение квантовых состояний по энергии N(E). Равномерность состояний по энергии не постоянна.

Рассмотрим кристалл с единичным объёмом, для этого кристалла известны все квантовые состояния в энергетической зоне. Число квантовых состояний dz, приходящееся на интервал энергии dE, то плотность квантовых состояний:

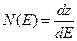
N(E) определяет число квантовых состояний, приходящееся на единицу энергии к единице объёма.

Плотность квантовых состояний N(E) определяется следующим соотношением:

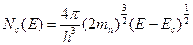(1)

В кристалле электроны взаимодействуют со всеми: ионами, дырками и др. Будем считать, что он не взаимодействует ни с кем (как в вакууме), но это взаимодействие загоним в величину m_n (т.е. электрон обладает уже другой массой по сравнению с электроном в вакууме)

Выражение (1) определяет число квантовых состояний, приходящихся на единицу объёма п/п и единичный интервал энергии dE.

Можно записать для плотности квантовых состояний для дырок (вv-зоне) выражение:

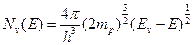(2)

(1) и (2) – плотности квантовых состояний, в которых могут находится электроны в с-зоне и дырки в v-зоне.

2.Система многих частиц описывается функцией распределения f(E,T), определяющей вероятность того, что уровень с энергией E занят электронами при некоторой температуре Т. Если известна плотность квантовых состояний N(E), то произведение N(E)*dE*f(E)=dn – концентрация носителей заряда, обладающих энергией, заключенной внутри dE (например, концентрация электронов n в интервале от E₁ до Е₂ будет равна:

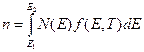(3)

В п/п характер распределения подвижных носителей заряда по энергии описывается квантовой функцией Ферми-Диррака.

Функция Ферми-Диррака:

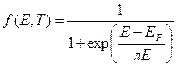(4)

где E_F – уровень или энергия Ферми

В частных случаях функция Ферми-Диррака преобразуется классической функцией Максвелла-Больцмана.

Функция Максвелла-Больцмана:

(5)

с – константа для определения проводника и определения температуры

Рассмотрим характер заполнения электронами энергетических состояний в соответствии с температурой.

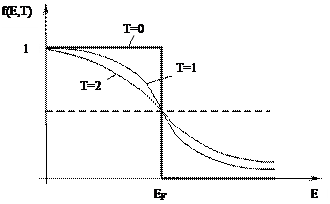Все энергетические состояния с энергией Е<Е_F имеют f(E,T)=1 – заполнены электронами, а при E>E_F – не имеют электроны, для них f(E,T)=0. Т₂>Т₁.

При заданной температуре (не нулевой) существует вероятность, что существует количество электронов, расположенных????? уровня Ферми.

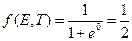- вероятность заполнения электронами

Для электронов, заполняющих энергетические состояния Е >> состояния E_F можно пренебречь в (5) единицей по сравнению с exp. Следовательно получим выражение, которое и есть функция Максвелла-Больцмана.

Вернёмся к (3)

В зоне с Е₁=Е_е (край с-зоны)

Если Е>>E_F, систему частиц можно описать функцией распределения Максвелла-Больцмана. Такая система называется насыщенной.

Если Е>>Е_F не выполняется, то такая система частиц является вырожденной, а такой п/п – вырожденный.

В вырожденном п/п уровень Ферми должен быть в разрешённой зоне. Функция Ферми-Диррака при больших значениях энергии уменьшается очень быстро и стремится к 0. Поэтому верхний предел интегрирования в уравнении (3) можно принять равным бесконечности, а нижний предел должен соответствовать?ну зоны с или Е_е. Соотношение (3) примет вид:

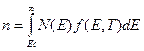(6)

Концентрация электронов в с-зоне (проводимости) приходящийся на энергетический интервал dE, будет равна:

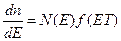
Построим графически зависимость плотности квантовых состояний от энергии, dn/dE, температуры от энергии.

Наша концентрация электронов в с-зоне соответствует заштрихованная

область (ее площадь). В выражение (в) нужно подставить выражение для

плотности квантовых состояний N(E) (1),подставить функцию Ф-Д, предпо-

ложив что exp>>1. После интегрирования получим окончательное выражение

для концентрации подвижных электронов в c-зоне.

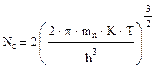
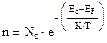
Где N_c–эффективная плотность состояний для электронов в с-зоне.

K-постоянная Больцмана

M_n-эффективная масса

Концентрация подвижных дырок в валентной зоне может быть рассчитана

аналогично E₀-край V-зоны.

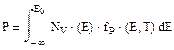
N_v(E)-плотность квантовых состояний в валентной зоне проводника

F_p(E₁T)-функция распределения подвижных дырок

Концентрация дырок в валентной зоне:p=N_vexp

N_v-плотность квантовых состояний для дырок имеет следующий вид:

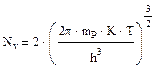
Определим (рассчитаем) положение уровня Ферми сначала в собственном

полупроводнике n = p = собственной концентрации- n_i.

Подставим n и p, полученные ранее.

Дата добавления: 2014-01-06