Области линейной и нелинейной рекомбинации

Чем больше дырок на уровне, тем меньше электронов.

При возрастании уровня инжекции t_n=t_p

u_n=u_p

Dn=Dp

Членом N(f-f₀) можно пренебречь.

Получили математическую модель, позволяющую прогнозировать поведение времени жизни от уровня инжекции на одном уровне центров.

Назовём границы линейной рекомбинации Dn₁ и Dn₂ .

Линейная рекомбинация при низком уровне инжекции будет идти при Dn < Dn₁, тогда t_n,t_p=const

u_n=(1/t_n)Dn

Следовательно линейная рекомбинация.

При Dn > Dn₁, t_n,t_p=const

Область нелинейной рекомбинации имеет место, когда Dn₁<n<Dn₂. Нужно получить аналитическое выражение для границ области нелинейной рекомбинации Dn₁ и Dn_1. Пусть рекомбинация носителей на центре при низком уровне инжекции линейна (t - пост). Если изменение вероятности заполнения электронами центра за счёт увеличения уровня инжекции не превышает 50% по отношению к равновесному заполнению. Выражение, с помощью которого определяют нижнюю границу области нелинейной рекомбинации:

		+		-

либо то, либо другое

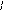
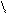
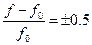
Если f>f₀, то +0.5; если f<f₀, то –0.5.

Вместо функции f подставляем выражение (4) и будем решать полученное уравнение относительно Dn. То что найдём, Dn нижняя граница нелинейной рекомбинации. Это выражение для Dn₁ будет иметь вид:

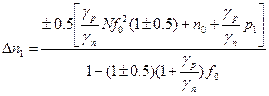
N – концентрация дефектов;

f₀ – равновесная функция Ферми-Диррака.

При Dn < Dn₁, t_n,t_p=const – рекомбинация линейная.

Вторая область линейной рекомбинации наблюдается, когда Dn > Dn_2.

Найдём верхнюю границу области. Будем считать рекомбинацию носителей на центре линейной (t-постоянная), если неравновесная стационарная функция заполнения f отлична от своего предельного значения, задаваемого асимметрией сечения захвата не более чем на 50%.

Уравнение, из которого будем определять верхнюю границу области нелинейной рекомбинации:

(f–f_пр)/f_пр=±0.5

f<f_пр, то –0.5

f>f_пр, то +0.5

В уравнение вместо f_пр подставим значение:

f_пр=g_n/(g_n+g_p)

а вместо f подставляем уравнение (4).

Решаем полученное уравнение относительно Dn, это и будет верхняя граница области нелинейной рекомбинации:

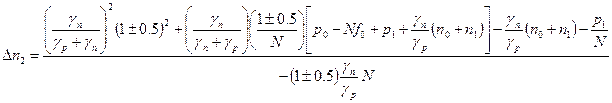
В конкретных ситуациях эти выражения существенно уменьшаются. Для акцепторного центра g_p>g_n, т.е. есть уменьшается температура, уровень Ферма выше уровня дефекта, тогда

Dn₁=n/2

Dn₂=3N+2n₀

n₀-удельное сопротивление материала.

Дата добавления: 2014-01-06