Амплитудно-частотная характеристика (АЧХ)

-- Зависимость коэффициента усиления усилителя от частоты усиливаемого сигнала

K _U = F( ω )

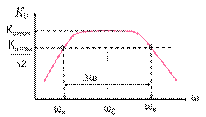
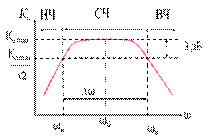
∆ω = ω_в – ω_н - полоса пропускания

ω₀ – частота, на которой коэффициент максимальный

ω_н – частота среза в области низких частот

ω_в – частота среза в области высоких частот.

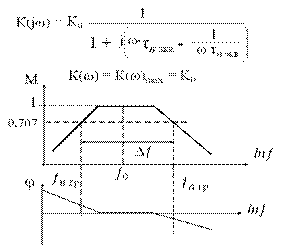
Принято АЧХ представлять в нормированном виде М(ω) = K_U / K_{U max}

K_U – текущее значение коэффициента передачи

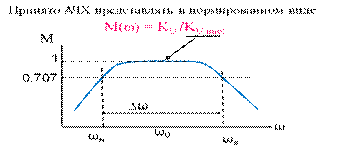
На частоте ω₀ K_U = К_Umax и М = 1. 1 / √2 = 0,707

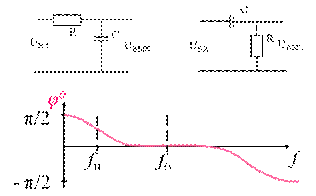
6.9.2 Фазочастотная характеристика (ФЧХ) φ = F(ω)

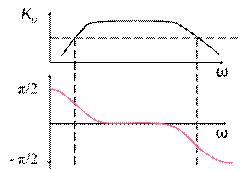
6.9.3 Переходная характеристика

Эту характеристику можно рассматривать как зависимость коэффициента усиления от времени.

В этом случае К(t) = (1 – e ^{- t/τ})

Амплитудно-частотную АЧХ и фазочастотную ФЧХ характеристики рассмотреть и изучить при выполнении домашней работы. «Расчет усилителя с RC-связями». Изучить частотные параметры усилителя.

Из курса ОТЦ вспомнить, что такое частота среза и как она связана с постоянной времени.

T = 1/ f

Если частота f = 50 Гц, то чему равен период Т и чему рана круговая частота ω.

Домашнее задание № 7

1. Какому типу RC-цепи соответствует АЧХ и ФЧХ в области НЧ и ВЧ.

2. При каких условиях К₀ не зависит от частоты, а фазовый сдвиг равен нулю.

Домашнее задание № 8

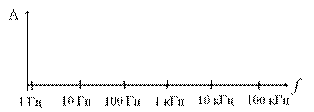
1. Изобразить АЧХ своего голоса и слуха.

Определение параметров усилителя

Упрощение схемы:

- Выходная цепь,

- Эмиттерная цепь,

Входная цепь.

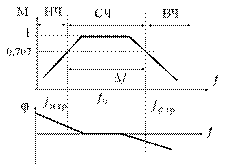
Рассмотрим три поддиапазона частот или времен

- НЧ – большие времена,

- СЧ – средние времена,

- ВЧ – малые времена.

T = 1/ f

Выходная цепь

Примем С_Э → ∞ Х_Сэ → 0, r_э << r_К

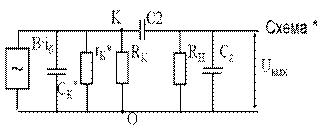
На основе теоремы об эквивалентном генераторе преобразует схему относительно точек «К – О».

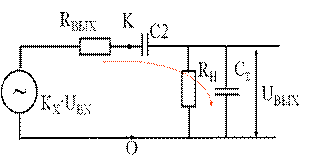
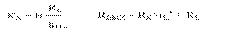
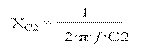
Емкость C2 >> C_∑ , поэтому их влияние можно рассматривать раздельно.

Средние частоты

Х_С2 << (R_ВЫХ + R_H), (Х_Ск^* + Х_Сн) >> R_H

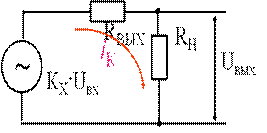
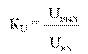
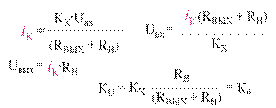
Коэффициент К - нечастотнозависимый

Низкие частоты

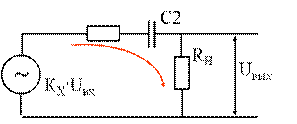
Х_С2 ≈ (R_ВЫХ + R_H), (Х_Ск^* + Х_Сн) >> R_H

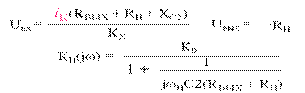
C2·(R_ВЫХ + R_H) = τ_н τ_н – постоянная времени в области низких частот (НЧ)

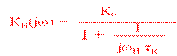
ω_Н – н – символ принадлежности частоты к области низких частот.

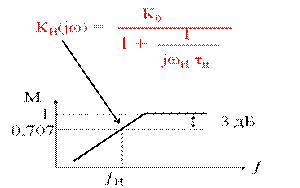
Входная цепь

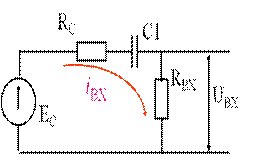
Влияние входной цепи оценим через постоянную времени τ_вх

C1·(R_ВХ + R_С) = τ_вх

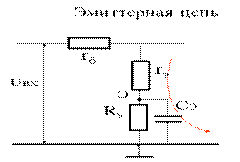
Z_Э = r_Э + R_Э//X _Сэ r_Э << R_Э R_Э >> X _Сэ

Влияние эмиттерной цепи оценим τ_Э ≈ r_Э·С_Э

Таким образом, каждая из емкостей С1, С2, С_Э влияет в области НЧ причем структура соотношений одинаковая. Для оценки их совместного влияния введем понятие эквивалентной постоянной времени в области НЧ τ_{н экв}

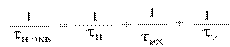
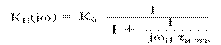
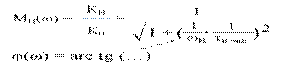
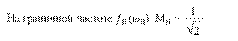
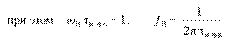
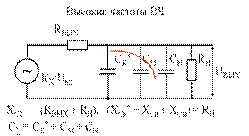
Введем τ _в = С_∑·(R_ВЫХ//R_Н)

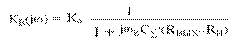
Кроме распределенной емкости на ВЧ влияет зависимость коэффициента В от частоты.

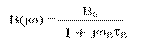
В области ВЧ также можно ввести эквивалентную постоянную времени

τ _{в ЭКВ} = τ _в + τ_В

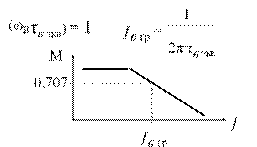
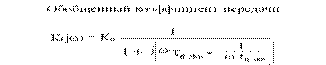
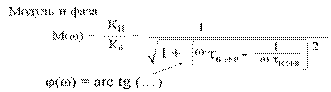
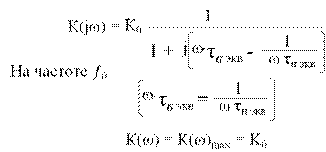
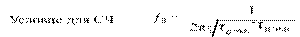
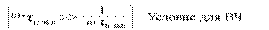
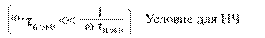
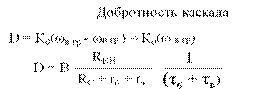
Для современных транзисторов τ_в << τ _{в .}.

Учтем также, что В >> 1, Rc << Rвх, r_б >> r_э.

Для современных ИМС определяющим является емкость С_К = (В + 1)·С_К.

τ _в ≈ В С_К(R_вых //R_Н)

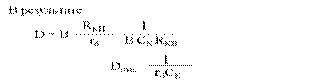
Многокаскадные усилители

Пусть имеется N одинаковых каскадов.

Дата добавления: 2014-01-07