Квазистационарные монохроматические электромагнитные поля

Уравнения электромагнитного поля в квазистационарном приближении имеют вид:

rot 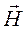= σ, (24.1)

rot = -. (24.2)

В уравнение (24.1) не входит явным образом вектор и параметр ε, следовательно, можно сделать вывод, что квазистационарное электромагнитное поле не зависит от диэлектрической проницаемости среды.

Предположим, что зависимость электромагнитного поля от времени выражается экспоненциальным множителем e^-iωt. Тогда получим уравнения для комплексных векторов поля:

rot 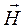= σ, (24.3)

rot = iωμ. (24.4)

В данной системе поля и взаимосвязаны, однако для решения практических задач удобнее иметь дело с уравнениями, в которые поля и входили бы порознь.

Разделение полей возможно, если в некоторой области пространства удельная электрическая проводимость σ и магнитная проницаемость μ постоянны.

Векторы и удовлетворяют уравнениям:

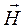∆+ iωμσ= 0, (24.5)

∆+ iωμσ= 0. (24.6)

Введем обозначение

k² = iωμσ. (24.7)

Тогда уравнения (22.5) и (22.6) примут вид:

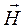∆+ k²= 0, (24.8)

∆+ k²= 0. (24.9)

Уравнения (22.8) и (22.9) называются уравнениями Гельмгольца.

Параметр k, определяемый соотношением

k = = 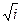· (24.10)

носит название волнового числа среды.

Исследуем волновое число k.

Для извлечения корня из i представим эту величину в экспоненциальной форме, воспользовавшись формулой Эйлера:

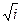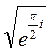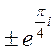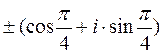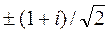= = = = . (24.11)

Для определенности выберем то значение корня, при котором

Re k > 0, Im k > 0, (24.12)

т.е. k = 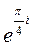= (1 + i) 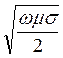. (24.13)

Введем обозначение 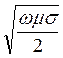= . (24.14)

Тогда k = (1 + i)·. (24.15)

Определим размерности λ и k, учитывая, что ω = 2πf = 2π/T, где f – частота колебания в Гц, Т – период а с, σ = 1/ρ (1/(Омм), и полагая μ равной магнитной проницаемости вакуума μ = μ₀ = 4π·10^-7 (Ом·с)/м:

λ = (24.16)

Следовательно, λ измеряется в метрах, а k – в 1/м.

Применим теорию квазистационарного электромагнитного поля к решению фундаментальных для электроразведки задач - иссле­дованию распространения плоских электромагнитных волн в однородной среде.

Пусть задана однородная изотропная проводящая среда с параметрами σ и μ. Введем в ней декартову систему координат XYZ (ось Z направлена вертикально вниз). Пусть в этой среде распространяется квазистационарное, гармоническое во времени поле 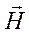, , обладающее следующими свойствами.

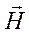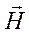1. Вдоль любой горизонтальной плоскости векторы , постоянны, т.е ≡ const, ≡ const при z = const. (24.17)

2. Поле исчезает с ростом z, т.е.

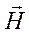, → 0 при z → ∞. (24.18)

Ввиду (24.17) имеем:

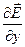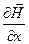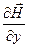≡ ≡ ≡ ≡ 0. (24.19)

Откуда

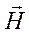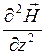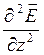∆= ; ∆ = ; (24.20)

Следовательно, уравнения Гельмгольца для векторов 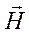и приобретают вид

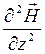+ k²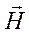= 0, (24.21)

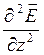+ k² = 0. (24.22)

Уравнения (24.21) и (24.22) носят название одномерных уравнений Гельмгольца.

Решения этих уравнений записы­ваются в виде:

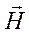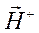= e^ikz + e^-ikz, (24.23)

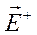= e^ikz + 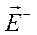e^-ikz, (24.24)

где 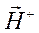, , , 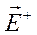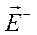- некоторые постоянные (в общем случае комплексные) векторы, которые необходимо определить. Для этого рассмотрим экспоненты e^ikz, e^-ikz:

e^ikz = exp(-z)exp(iz), (24.25)

e^-ikz = exp(z)exp(-iz). (24.26)

Поскольку 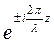= cos(z) ± isin(z) - функция, ограниченная по z, ясно, что e^ikz → 0 при z → ∞, a e^-ikz → ∞ при z → ∞. Итак для того чтобы удовлетворялось условие задачи (24.18), необходимо в (24.23) и (24.24) положить

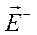= 0, = 0.

Окончательно получаем:

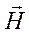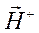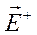=e^ikz, = e^ikz. (24.27)

Теперь разложим векторы 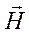и по декартовому базису ,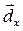

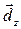, . Тогда векторные равенства (24.27) можно записать в виде системы скалярных равенств.

Например, для магнитного поля имеем:

H_x = H_x⁺e^ikz, H_y = H_y⁺e^ikz, H_z = H_z⁺e^ikz, (24.28)

Аналогично, для электрического поля имеем:

Е_x = Е_x⁺e^ikz, Е_y = Е_y⁺e^ikz, Е_z = Е_z⁺e^ikz. (24.29)

Дата добавления: 2014-01-07