Проектирование типовых планетарных механизмов

Краткое содержание: Постановка задачи синтеза планетарных механизмов. Условия подбора чисел зубьев. Вывод расчетных формул для условий соосности, соседства и сборки. Подбор чисел зубьев методом неопределенных коэффициентов (метод сомножителей). Пример. Планетарные механизмы с двумя подвижностями (дифференциалы). Кинематическое исследование дифференциала с замыкающей цепью.

Постановка задачи синтеза планетарных механизмов

При проектировании многопоточных планетарных механизмов необходимо, кроме требований технического задания, выполнять ряд условий связанных с особенностями планетарных и многопоточных механизмов. Задача проектирования и в этом случае может быть разделена на структурный и метрический синтез механизма.

- при структурном синтезе определяется структурная схема механизма,

- при метрическом - определяются числа зубьев колес, так как радиусы зубчатых прямо пропорциональны числам зубьев .

Для типовых механизмов первая задача сводится к выбору схемы из набора типовых схем. При этом руководствуются рекомендуемым для схемы диапазоном передаточных отношений и примерными оценками ее КПД.

После выбора схемы механизма необходимо определить сочетание чисел зубьев его колес, которые обеспечат выполнение условий технического задания - для редуктора это передаточное отношение и величина момента сопротивления на выходном валу. Передаточное отношение задает условия выбора относительных размеров зубчатых колес - чисел зубьев колес, крутящий момент задает условия выбора абсолютных размеров - модулей зубчатых зацеплений. Так как для определения модуля необходимо выбрать материал зубчатой пары и вид его термообработки, то на первых этапах проектирования принимают модуль зубчатых колес равным единице, то есть решают задачу кинематического синтеза механизма в относительных величинах.

При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при заданном числе силовых потоков (или числе сателлитов) и заданном передаточном отношении необходимо подобрать числа зубьев колес, которые обеспечат выполнение всех условий, накладываемых на многосателлитные зубчатые механизмы.

Условия подбора чисел зубьев

Условия, которые необходимо выполнить при подборе чисел зубьев колес типового планетарного механизма:

1. заданное передаточное отношение с требуемой точностью
2. соосность входного и выходного валов механизма
3. свободное размещение (соседство) сателлитов
4. сборку механизма при выбранных числах зубьев колес
5. отсутствие подреза зубьев с внешним зацеплением
6. отсутствие заклинивания во внутреннем зацеплении
7. минимальные относительные габариты механизма.

Вывод расчетных формул для условий соосности, соседства и сборки

Рассмотрим эти условия подробнее на примере двухрядного планетарного механизма с одним внешним и одним внутренним зацеплением.

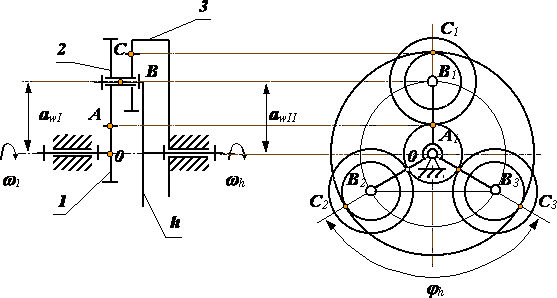
1. Обеспечение заданного передаточного отношения с требуемой точностью:

Принимаем требуемую точность ± 5%, тогда для рассматриваемой схемы механизма с учетом формулы Виллиса передаточное отношение определяется:

,

,

где 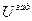- заданное передаточное отношение, 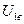- передаточное отношение редуктора, для которого выполняются все условия, накладываемые на многосаттелитные редукторы.

1. Обеспечение соосности входного и выходного валов:

Для этого необходимо чтобы межосевое расстояние в передаче внешнего зацепления (первый ряд) равнялось межосевому расстоянию в передаче внутреннего зацепления (второй ряд), то есть

Обычно в планетарных механизмах применяются зубчатые колеса без смещения, для которых 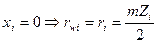Тогда

.

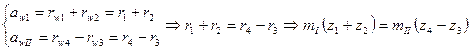Принимаем, что , и получаем условие соосности для данной схемы механизма:

1. Обеспечение условия соседства сателлитов (при числе сателлитов ):

Условие соседства – это условие совместного размещения нескольких сателлитов по общей окружности в донной плоскости и требует, чтобы при многосателлитной конструкции соседние сателлиты не задевали друг друга. Для этого необходимо назначить числа зубьев таким образом, чтобы расстояние между осями соседних сателлитов 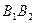было бы больше, чем диаметр окружности вершин наибольшего из сателлитов (в условиях данного примера - 2). Т.е

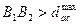
Учитывая, что 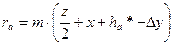, а для зубчатых колес без смещения 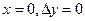запишем диаметр окружности вершин: .

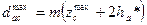Расстояние между осями соседних сателлитов запишем из ,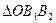

где 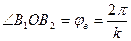- угол водила,

, где знак «+» соответствует внешнему зацеплению солнечного колеса и сателлита, «-» - внутреннему.

.

Окончательно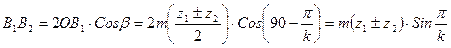

Подставим полученные выражения в неравенство и получим условие соседства:

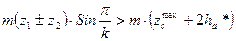, откуда:

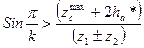
1. Обеспечить возможность сборки механизма с подобранными числами зубьев колес при заданном числе сателлитов

Для вывода формулы условия сборки воспользуемся следующим методом:

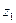Допустим, что все сателлиты устанавливаются на оси водила в одном и том же положении - точке . После установки первого сателлита, зубья колес и 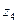определенным образом установились относительно зубьев венцов сателлита. Тогда установить второй сателлит в этом же положении будет можно, если после поворота водила на угол колесо 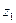повернется на целое число угловых шагов 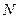. При этом зубья колес 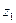и 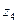установятся относительно зубьев венцов сателлита так же, как и при установке первого сателлита.

При установке второго сателлита водило нужно повернуть минимум на угол водила 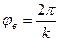а также можно добавить к нему любое целое число оборотов водила , т.е угол изменится на величину .

Угол поворота солнечного колеса после поворота водила можно записать следующим образом: .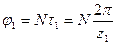

Тогда передаточное отношение редуктора может быть записано:

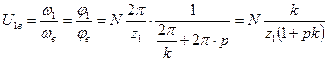
Формула для условия сборки примет следующий вид:

1. Обеспечить отсутствие подрезания колес с внешними зубьями зубьев:

Это условие обеспечивается, если для всех колес с внешними зубьями выполняется неравенство .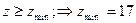

1. Обеспечить отсутствие заклинивания во внутреннем зацеплении:
   Это условие для передачи внутреннего зацепления, состоящей из колес без смещения, можно обеспечить при выполнении следующих неравенств

1. Обеспечить минимальные габариты механизма.

Подбор чисел зубьев методом неопределенных коэффициентов (метод сомножителей)

Рассмотрим один из методов, используемых при подборе чисел зубьев планетарного редуктора, - метод сомножителей. Метод позволяет объединить в расчетные формулы некоторые из условий подбора (условия 1, 2, 5 и 6). Выполнение остальных условий для выбранных чисел зубьев проверяется. Из первого условия выразим внутреннее передаточное отношение механизма. Внутренним называют передаточное отношение механизма при остановленном водиле, то есть механизма с неподвижными осями или рядного механизма.

Для рассматриваемой схемы:

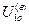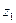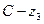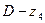Разложим внутреннее передаточное отношение на сомножители - некоторые целые числа . При этом сомножитель соответствует числу зубьев, , и . Сомножители могут быть произвольными целыми числами, комбинация 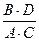которых равна .

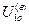Для рассматриваемой схемы желательно придерживаться следующих диапазонов изменения отношений между сомножителями

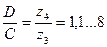-внешнее зацепление, - внутреннее зацепление.

Включим в рассмотрение условие соосности: и выразим его через сомножители

,

где - неопределенные коэффициенты. Если принять, что коэффициенты равны соответственно , , то выражение превращается в тождество. Из этого тождества можно записать:

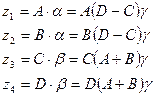
где - произвольный множитель, выбором которого обеспечиваем выполнение условий 5 и 6.

Зубья колес планетарного механизма, рассчитанные по этим формулам, удовлетворяют условиям 1, 2, 5 и 6.

Проверяем эти зубья по условиям 3 (соседства) и 4 (сборки) и если они выполняются, считаем этот вариант одним из возможных решений. Если после перебора рассматриваемых сочетаний сомножителей получим несколько возможных решений, то проводим их сравнение по условию 7.

Решением задачи будет сочетание чисел зубьев, обеспечивающее габаритный минимальный размер

Рассмотрим подбор чисел зубьев многосателлитного редуктора на примере двухрядного планетарного редуктора со смешанным зацеплением.

Пример: Двухрядный планетарный редуктор со смешанным зацеплением

Исходные данные:

- передаточное отношение

- число сателлитов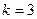

- модуль колес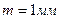

Постановка задачи:

- подобрать числа зубьев колес планетарного редуктора, удовлетворяющие всем условиям, накладываемым на многосателлитные планетарные редукторы, причем минимальных размеров.

- рассчитать радиусы колес планетарного редуктора, начертить схему.

Дата добавления: 2014-01-07