Формула Лагранжа

Если функция непрерывна на замкнутом промежутке [ a, b ] и дифференцируема на открытом промежутке (a, b), то можно найти такую точку c, принадлежащую промежутку (a, b), для которой справедливо равенство:

f (b) – f (a) = f¢ (c)(b - a). (1)

Эта формула называется формулой конечных приращений Лагранжа. Проведем наглядное обоснование этой формулы. Возьмем на графике функции f (x) точки A (a; f (a)) и B (b; f (b)). Проведем через эти точки прямую AB. Проведем также прямую L, параллельную прямой AB, так, чтобы она не пересекала график функции f (x) на промежутке (a, b). Сохраняя параллельность L и AB, будем "надвигать" прямую L на график f (x) до тех пор, пока прямая L не коснется графика f (x) в некоторой точке c промежутка (a, b). Геометрическую точку касания обозначим буквой M, а через MN обозначим касательную к графику f (x), параллельную прямой AB. Очевидно, угловые коэффициенты прямых MN и AB (то есть тангенсы углов наклона прямых к оси абсцисс) равны. Угловой коэффициент прямой MN равен f¢ (c), а угловой коэффициент прямой AB равен (f (b) – f (a))/(b-a), и справедлива формула:

.

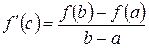Отсюда сразу получается формула (1). На приведенном рисунке видно, что могут существовать другие точки, принадлежащие промежутку (a, b), в которых касательные к графику функции f (x) параллельны прямой MN. Производную функции f (x), вычисленную в любой из этих точек, можно подставить в правую часть формулы (1) вместо множителя .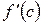

Сформулируем теорему о монотонности функции. Если f¢ (x) > 0 на промежутке (a; b), то на (a; b) функция f (x) возрастает. Если f¢ (x) < 0 на промежутке (a; b), то на (a; b) функция f (x) убывает.

Докажем эту теорему. Пусть t ₁ и t ₂ — любые числа из промежутка (a; b), причем t ₂> t ₁. Тогда по теореме Лагранжа можно указать такое число c из промежутка (t ₁; t ₂), для которого справедливо равенство f (t ₂) – f (t ₁) = f¢ (c)(t ₂ – t ₁). Если f¢ (x) > 0 для всех x из промежутка (a; b), то f¢ (c) > 0, и из условия t ₂ > t ₁ следует, что f (t ₂) – f (t ₁) > 0. Таким образом, возрастание функции f (x) на промежутке (a; b) доказано. Аналогично доказывается вторая часть теоремы.

Дата добавления: 2014-01-07