Диполь в электрическом поле

Расчет прочности зубьев по контактным напряжениям.

Расчёт прямозубых цилиндрических передач на прочность

Геометрические параметры

У косозубых колес зубья направлены не по образующей делительного цилиндра, а составляют с ней некоторый угол β [бэта].

С увеличением угла наклона β [бэта] увеличивается плавное зацепление и нагрузочная способность передачи, но при этом увеличивается и осевая сила, которая дополнительно нагружает подшипники. Поэтому угол β ограничивают в пределах от 7º до 20º.

Основные геометрические размеры зависят от модуля и числа зубьев. В этих передачах учитывают два шага: нормальный шаг зубьев P_n – в нормальном сечении и окружной шаг P_t – в торцевом сечении.

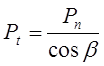
Соответственно два шага учитывают два модуля: окружной модуль m_t и нормальный модуль m_n.

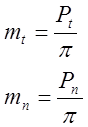
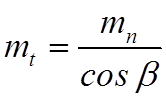
Делительный диаметр вычисляется по формуле

Диаметр вершин зубьев

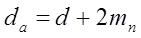
Межосевое расстояние

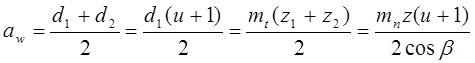
Прочность зуба определяют его размеры и форму нормального сечения. Форму косого зуба в нормальном сечении принято определять через параметры эквивалентного прямозубого колеса.

Эквивалентное число зубьев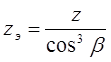

Силы в зацеплении определяются в полюсе зацепления П. Сила нормального давления F_n зуба шестерни на зуб колеса направлена по линии зацепления эквивалентного прямозубого колеса. Ее раскладывают на три составляющие:

окружную силу ;

радиальную силу ;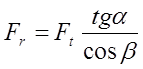

осевую силу .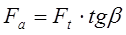

Наличие в зацеплении осевых сил, которые дополнительно нагружают валы и подшипники, является недостатком косозубых передач.

3. «Шевронная передача»

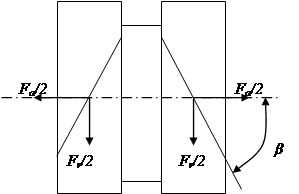Недостаток косозубой передачи можно устранить шевронной передачей, которая подобна удвоенной косозубой передачи с противоположным направлением зубьев. Осевые силы здесь уравновешиваются на самом зубчатом колесе .

Применяют в высоконагруженных передачах. Шевронные колеса изготовляют с дорожкой в середине колеса для выхода режущего инструмента или без дорожки.

4. «Виды разрушения зубьев»

Плакат «критерии работоспособности зубчатых колес»

При передачи нормального вращения в зацеплении действует нормальная сила F_n и сила трения R_f, связанная со скольжением. Под действием этих сил зуб находится в сложном, напряженном состоянии. Решающее влияние на работоспособность зуба оказывают контактное напряжение σ_Н [сигма] и напряжения изгиба σ * _F [сигма].

* Индекс F приписывается параметрам, связанным с расчетом по напряжениям изгиба, который выполняют по ножке зуба.

Излом зубьев происходит при перегрузках, а также под действием переменных напряжений изгиба, вызывающих усталость материала зубьев. Усталостные трещины образуются чаще всего у основания зуба на той стороне, где от изгиба возникают наибольшие напряжения растяжения. Для предупреждения усталостного излома ограничивают напряжение изгиба, принимают колеса со смещением, увеличивают точность изготовления и монтажа передачи.

Излом зубьев – основная причина выхода из строя зубьев открытых передач.

Усталостное разрушение рабочих поверхностей зубьев – основной вид разрушения зубьев закрытых передач.

Износ зубьев характерен для открытых и закрытых, работающих в загрязненной среде. Происходит в результате попадания на зубья абразивных частиц (пыли, грязи, песчинок и др.).

Заедание зубьев происходит преимущественно в высоконагруженных быстроходных передачах. В месте контакта зубьев развиваются высокие давления и температура, масляная пленка разрывается и появляется металлический контакт. Здесь происходит как бы сваривание частиц металла с последующим отрывом их от менее прочной поверхности. Образовавшиеся наросты на зубьях задирают поверхности других зубьев, оставляя на них широкие и глубокие борозды в направлении скольжения. Заедание может завершиться прекращением относительного движения. Для предупреждения заедания понижают шероховатость поверхностей зубьев, повышают их твердость и применяют противозадирные масла.

Расчёт на прочность прямозубых и косозубых цилиндрических передач стандартизирован ГОСТ 21354. В данном конспекте лекций введены некоторые упрощения, мало влияющие на результаты расчётов для большинства практических случаев.

4.6. Расчетная нагрузка

За расчетную нагрузку принимают максимальное значение удельной нагрузки, распределенной по линии контакта зубьев:

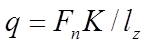
где F_n —нормальная сила в зацеплении;

K = K_bK_V —коэффициент расчетной нагрузки;

K_b —коэффициент концентрации нагрузки;

K_v —коэффициент динамической нагрузки;

l_z —суммарная длина линии контакта зубьев.

Концентрация нагрузки и динамические нагрузки различно влияют на прочность по контактным и изгибным напряжениям. Соответственно различают K_H, K_Hβ, Khv при расчетах по контактным напряжениям и К_F, К_Fβ, К_{F V} —по напряжениям изгиба.

Коэффициент концентрации нагрузки K_b. Концентрация или неравномерность распределения нагрузки по длине зуба связана с деформацией валов, корпусов, опор и самих зубчатых колес, а также с погрешностями изготовления монтажа передачи.

Коэффициент динамической нагрузки K_V. Данный коэффициент учитывает погрешности в изготовлении зубьев колёс по шагу и профилю, которые явно непропорционально проявляются с увеличением частоты вращения колёс (окружной скорости).

Точный расчёт данных коэффициентов довольно сложен и их рекомендуется выбирать из справочной литературы по расчёту зубчатых передач.

Исследованиями установлено, что наименьшей контактной усталостью обладает околополюсная зона рабочей поверхности зубьев, где наблюдается однопарное зацепление — см. рис. 8.5. Поэтому расчет контактных напряжений принято выполнять при контакте в полюсе зацепления (рис. 4.3). Контакт зубьев можно рассматривать как контакт двух цилиндров с радиусами р₁ и р₂. При этом контактные напряжения определяют по формуле

для прямозубых передач с учетом формул (4.4)...(4.6):

q = F_nK_H/b_w = F_tK_H/(b_w cos a_w) = 2T₁K_H/(d_wlb_w cos a_w).

Радиусы кривизны эвольвент зубьев в точке контакта

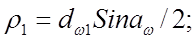
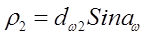
По формуле (4.3):

Где 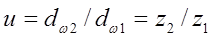, знак «+» для наружного, а «—» для внутреннего зацепления.

Подставляя в формулу (4.7) и заменяя 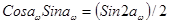, получаем

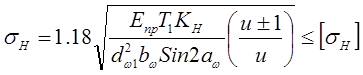
Данная формула определения контактных напряжений является классической. Гост 21354 даёт другую формулу, где ряд коэффициентов имеют иной вид, но она построена на базе формулы 4.10. В различных учебных пособиях и расчётных электронных программах эта формула также может быть представлена в ином виде и поэтому, если Вы выполняете расчет по одному из выбранных пособий, то значения коэффициентов необходимо принимать только из этого пособия.

Значения расчетных контактных напряжений одинаковы для шестерни и колеса. Поэтому расчет выполняют для того из колес пары, у которого меньше допускаемое напряжение [σ_н] (чаще это бывает колесо, а не шестерня).

Формулу (8.10) используют для проверочного расчета, когда все необходимые размеры и другие параметры передачи известны. При проектном расчете необходимо определить размеры передачи по заданным основным характеристикам: крутящему моменту Т₁ или Т₂ и передаточному числу и. С этой целью формулу (4.10) решают относительно d₁ или а. Другие неизвестные параметры оценивают приближенно или выбирают по рекомендациям на основе накопленного опыта. В нашем случае принимаем: 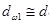, 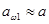=20°, (sin 2a0,6428), Кv 1,15 (этот коэффициент зависит от окружной скорости и, которая пока неизвестна, поэтому принято некоторое среднее значение — см. табл. 4.2). При этом из составляющих коэффициента Кн [см. формулу (4.4)] остается только Кн_β . Далее обозначаем — коэффициент ширины шестерни относительно диаметра. Подставляя в формулу (4.10) и решая относительно d_1, находим:

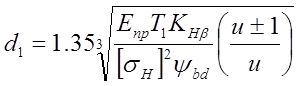(4.11)

Решая относительно межосевого расстояния a, заменяем ; 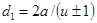и вводим 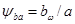- коэффициент ширины колеса относительно межосевого расстояния. После преобразований с учётом зависимости (4.12), 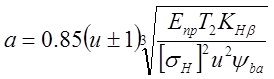. (4.13)

При расчёте передач с цилиндрическими зубчатыми колёсами чаще используют формулу (4.13), так как габариты передачи определяет преимущественно межосевое расстояние.

Ниже приводятся рекомендуемые значения стандартизированного межосевого расстояния и рекомендуемые передаточные числа редукторов.

Стандартные межосевые расстояния a_w:

1-й ряд —40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400...

2-й ряд—140, 180, 225, 280, 355, 450...

Стандартные значения : 0,1; 0,125; 0,16; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63; 0,8; 1,0; 1,25.

Стандартные номинальные передаточные числа u:

1-й ряд— 1,0; 1,25; 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3; 8,0;

2-й ряд— 1,12; 1,4, 1,8; 2,24; 2,8; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2 (допускаемое отклонение ±4%).

Выбор модуля и числа зубьев. В формуле (8.10) модуль и число зубьев непосредственно не участвуют. Они входят в эту формулу косвенно через d₁, который определяется произведением mz₁. Из этого следует, что значение контактных напряжений 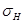не зависит от модуля или числа зубьев в отдельности, а определяется только их произведениями или диаметрами колес. По условиям контактной прочности при данном d₁ передачи может быть сколь угодно малым, лишь бы соблю­далось равенство mz₁=d₁.

Минимально допускаемое значение модуля можно определить из условий прочности зубьев на изгиб. Однако при таком расчете в большинстве случаев получают зацепления с очень мелкими зубьями, применение которых практически ограничено. Поэтому значение т обычно выбирают, ориентируясь на рекомендации, выработанные практикой, и затем проверяют на изгиб. В этих рекомендациях учитывают следующее.

Мелкомодульные колеса с большим числом зубьев предпочтительны по условиям плавности хода передачи (увеличивается ) и экономичности. При малых т уменьшаются потери на трение (уменьшается скольжение), сокращается расход материала (уменьшается наружный диаметр ) и экономится станочное время нарезания зубьев (уменьшается объем срезаемого материала).

Крупномодульные колеса с большим объемом зубьев дольше противостоят износу, могут работать длительное время после начала выкрашивания, менее чувствительны к перегрузкам и неоднородности материала (дефекты литья и т. п.). При мелком модуле возрастают требования к точности и жесткости передачи, так как увеличивается возможность поломки зубьев вследствие концентрации нагрузки, в особенности при перегрузках.

Практически рекомендуется принимать модуль зацепления в пределах и стремиться к меньшему его значению.

Электрическим диполем называется система двух одинаковых по величине разноименных точечных зарядов, расстояние между которыми значительно меньше расстояний до тех точек, в которых определяется поле диполя.

Прямая, проходящая через оба заряда, называется осью диполя (рис. 1).

Вектор, соединяющий заряды и направленный от отрицательного заряда к положительному, называется плечом диполя.

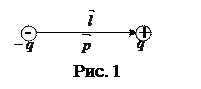Диполь характеризуется электрическим или дипольным моментом.

,

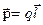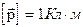
Электрический момент диполя (дипольный момент) - это вектор, численно равный произведению заряда диполя на его плечо и сонаправленный с плечом диполя.

В однородном электрическом поле (рис. 2) диполь будет поворачиваться и располагаться вдоль силовых линий. Силы, действующие на оба заряда, равны и противоположно направлены, такая пара сил лишь вращает диполь.

В неоднородном поле (рис. 3) силы имеют разную величину, поэтому диполь будет не только вращаться, но и втягиваться в область более сильного поля.

2. Поляризация диэлектриков. Напряженность поля в диэлектрике. Электрическое смещение .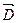

Диэлектриками (изоляторами) называются вещества, не способные проводить электрический ток. Диэлектрики не имеют свободных зарядов. Заряды, входящие в состав молекул диэлектрика, называются связанными. Под действием поля они могут немного смещаться из своих положений равновесия, но покинуть молекулу не могут.

Молекулы диэлектрика электрически нейтральны, т.к. содержат равное число положительных и отрицательных зарядов.

Диэлектрик называется неполярным, если электроны атомов в его молекулах расположены симметрично относительно ядер (Н₂, О₂, СС1₄). При этом центры тяжести положительных и отрицательных зарядов совпадают в отсутствие внешнего электрического поля () и дипольный момент молекулы равен нулю.

Диэлектрик называется полярным, если электроны располагаются несимметрично относительно ядер атомов, составляющих молекулу (Н₂О, НС1, NH₃). В таких молекулах центры тяжести положительных и отрицательных зарядов не совпадают, находясь, практически, на постоянном расстоянии друг от друга. Такие молекулы обладают постоянным дипольным моментом 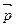и по своим электрическим свойствам подобны жестким диполям.

Действие внешнего электрического поля на полярную молекулу сводится, в основном, к стремлению повернуть молекулу так, чтобы ее дипольный момент ориентировался вдоль поля. На величину внешнее поле практически не влияет.

В неполярной молекуле под действием поля электрические заряды смещаются друг относительно друга, молекула приобретает дипольный момент, величина которого пропорциональна напряженности поля.

Таким образом, в отсутствии внешнего поля дипольные моменты молекул диэлектрика либо равны нулю (у неполярных), либо распределены в пространстве хаотически (у полярных), так что суммарный дипольный момент диэлектрика равен нулю.

Под действием внешнего поля вследствие ориентации дипольных моментов молекул диэлектрик поляризуется, результирующий дипольный момент диэлектрика становится отличным от нуля, на поверхности диэлектрика появляются связанные электрические заряды.

Поляризация диэлектрика означает, что результирующий дипольный момент диэлектрика становится отличным от нуля.

В качестве величины, характеризующей степень поляризации диэлектрика, естественно взять дипольный момент единицы объема. Если поле или диэлектрик (или они оба) неоднородны, степень поляризации в различных точках будет различна.

Вектором поляризации (поляризованностью) называется отношение дипольного момента малого объема DV диэлектрика к величине этого объема

.

Таким образом, поляризованность определяется дипольным моментом единицы объема диэлектрика.

У изотропных диэлектриков любого типа поляризованность прямо пропорциональна напряженности поля в той же точке:

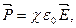
где - диэлектрическая восприимчивость диэлектрика, безразмерная, постоянная для данного диэлектрика величина.

По способности смешаться относительно положения равновесия под действием внешнего электрического поля заряды условно делят на свободные и связанные.

Свободными называют заряды, способные свободно перемещаться в теле под действием внешнего электрического поля (валентные электроны в проводниках, электроны и дырки в полупроводниках).

Связанными называют заряды, входящие в состав молекул диэлектриков, которые под действием внешнего электрического поля могут лишь смешаться из своего положения равновесия, но покинуть молекулу не могут.

Для установления количественных закономерностей поля в диэлектрике внесем в однородное внешнее электрическое поле пластину из однородного диэлектрика; при этом диэлектрик поляризуется (рис. 4), внутри диэлектрика возникает поле связанных зарядов ,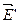

s - поверхностная плотность свободных зарядов,

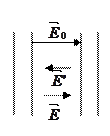s¢ - поверхностная плотность связанных зарядов.

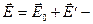результирующее поле внутри диэлектрика,

,

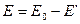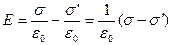. (1)

Т.к. по определению 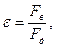а

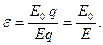
Диэлектрическая проницаемость среды 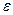показывает, во сколько раз напряженность электростатического поля в диэлектрике уменьшается по сравнению с вакуумом.

. (2)

Подставим (2) в (1):

,

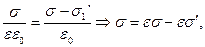
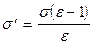. (3)

Подставим (3) в (2):

.

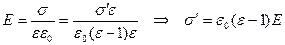Можно доказать, что .

Установим связь 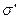с .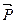

Полный дипольный момент пластинки диэлектрика (рис. 5) равен

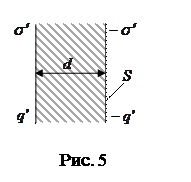
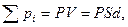
где S - площадь грани пластинки, d - ее толщина.

С другой стороны, пластинку можно рассматривать как диполь, полный дипольный момент которого равен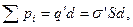

Таким образом, .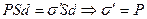

Поверхностная плотность связанных зарядов равна поляризованности диэлектрика .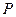

Установим связь между e и х.

Т.к. то

.

Помимо основного вектора 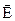в теории электричества оказывается необходимо ввести еще вектор электрической индукции 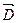(или вектор смещения).

Источником вектора 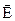служат свободные и связанные заряды.

Источником вектора 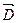служат только свободные заряды.

Как связаны между собой в однородном диэлектрике эти вектора?

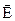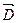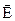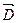Вектор представляет поле свободных и связанных зарядов, вектор - только поле свободных зарядов. Известно, что связанные заряды возникают из-за поляризации диэлектрика полем свободных зарядов. Поле связанных зарядов параллельно полю свободных, направлено в противоположную сторону и пропорционально ему, поэтому вектор и в однородном и изотропном диэлектрике должны быть параллельны и пропорциональны друг другу.

Поскольку в однородной среде с диэлектрической проницаемостью e поле свободных зарядов ослабляется средой в e раз, можно записать

,

где - коэффициент пропорциональности в СИ.

Таким образом, .

=1.

Векторы 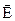и 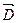в изотропном диэлектрике параллельны, но численно не совпадают, т.е. плотность линий разная.

Вектор электрической индукции 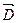равен произведению скалярной величины на вектор электрической напряженности.

Установим связь между .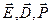

- характеризует поле свободных зарядов;

характеризует поле связанных зарядов;

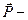характеризует поле свободных и связанных зарядов.

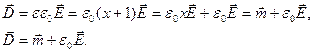
Дата добавления: 2014-01-07