Вершинное покрытие

Задача о клике.

Задача изоморфизма подграфу.

Задача о клике

Задача планирования работ

Задача о суммах элементов подмножеств.

Пусть у нас есть множество объектов различных размеров 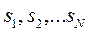и некоторая положительная верхняя граница L.

В задаче оптимизации необходимо найти набор объектов, сумма размеров которых наиболее близка к L и не превышает этой верхней границы.

В задаче принятия решения нужно установить, существует ли набор объектов с суммой размеров L.

Это упрощенная версия задачи об упаковке рюкзака.

Пусть у нас есть набор работ, и мы знаем время, необходимое для завершения каждой из них, 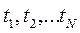, сроки 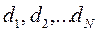к которым эти работы должны быть обязательно завершены, а также штрафы которые будут наложены при не завершении каждой работы в установленные сроки.

Задача оптимизации требует установить порядок работ, минимизирующий накладываемые штрафы.

В задаче принятия решений мы спрашиваем, есть ли порядок работ, при котором величина штрафа будет не больше Р.

Пусть дан граф G = G(V,E), где V – множество из n вершин, а E – множество ребер. Будем понимать под кликой максимальный по количеству вершин полный подграф в графе в G.

Задача состоит в определении клики в заданном графе G

Поскольку в полном графе на m вершинах имеется m(m-1)/2 ребер, то проверка, является ли данный граф полным, имеет сложность O (). Очевидно, что если мы рассматриваем подграф с m вершинами в графе G с вершинами (m < n), то всего существует различных подграфов. Если в задаче о клике количество вершин клики фиксировано, то перебирающий алгоритм имеет полиномиальную сложность:

Однако в общем случае придется проверять все подграфы с количеством вершин m = (2, n) на их полноту и определить максимальное значения m для которого в данном графе G существует полный подграф, что приводит к оценке в худшем случае:

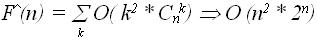
http://www.lektorium.tv/course/?id=22758

Даны 2 графа 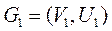и . Пусть 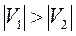Требуется ответить на вопрос: Найдется ли в графе подграф H, изоморфный графу ?

Дан граф G с m вершинами и целое положительное число n.

Граф называется кликой, если каждая вершина в нем связана ребром с каждой. Количество вершин в клике назовем ее мощностью.

Найдется ли в данном графе G клика мощности не менее, чем n?

Дан граф G с m вершинами и целое положительное число n.

Вершинным покрытием называется подмножество вершин графа 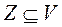, такое, что любое ребро графа G инцидентно хотя бы одной вершине множества Z.

Существует ли вершинное покрытие не более, чем из n вершин.

Дата добавления: 2014-01-07