Расчет прочности зубьев по напряжения изгиба

Зуб имеет сложное напряженное состояние. Наибольшие напряжения изгиба образуются у корня зуба в зоне перехода эвольвенты в галтель. Расчет носит приближенный характер. Вводят следующие допущения.

1) Вся нагрузка зацепления передается одной парой зубьев и приложена к вершине зуба

(справедливо для 7 и 8 степеней точности).

2) Зуб рассматриваем как консольную балку, для которой справедливы гипотеза плоских сечений или методы сопротивления материалов. Зуб подобен выступу, у которого размеры поперечного сечения соизмеримы с размерами высоты.

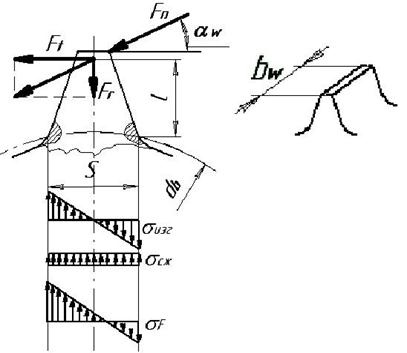
Рисунок 10 - Расчет зуба прямозубой цилиндрической передачи по напряжениям изгиба

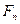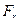Силу переносим по линии действия на ось симметрии зуба и раскладываем на составляющие и . Напряжение в опасном сечении, расположенном вблизи хорды основной окружности:

,

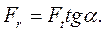
где W=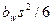- момент сопротивления сечения при изгибе; А=- площадь сечения.

Знак «-» указывает, что напряжение берут на растянутой стороне зуба, так как обычно здесь возникают трещины.

Значения l и s неудобны для расчетов. Используя геометрическое подобие зубьев различного модуля, эти величины выражают через безразмерные коэффициенты:

и ,

где m - модуль зубчатого зацепления.

После подстановки и введения расчетных коэффициентов получают

,

где 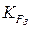- коэффициент расчетной нагрузки; 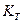- теоретический коэффициент концентрации напряжений.

Далее обозначают

-

-коэффициент формы зуба. Берут из рекомендаций в зависимости от z. Для колес с внутренними зубьями

Для прямозубых передач расчетную формулу записывают в виде

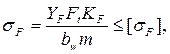
где - допускаемое напряжение изгиба.

Для проектных расчетов по напряжениям изгиба формулу решают относительно модуля путем замены , , , 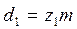тогда

.

И далее, принимая приближенно 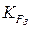=1,5 получают

Значениями и 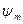задаются согласно рекомендациям.

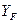- безразмерный коэффициент, значения которого зависят только от формы зуба и в том числе от формы его галтели. Форма зуба при одинаковом исходном контуре инструмента зависит от числа зубьев колеса z и коэффициента смещения инструмента x.

Обоснование выбора модуля (m) и числа зубьев (z)

Мелкомодульные колеса с большим числом зубьев предпочтительны по условиям плавности хода передачи (увеличивается 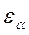) и экономичности. При малых m уменьшаются потери на трение, сокращается расход материала и экономится станочное время нарезания зубьев.

Крупно-модульные колеса с большим объемом зубьев дольше противостоят износу, могут работать длительное время после начала выкрашивания, менее чувствительны к перегрузкам и неоднородности материала. При мелком модуле возрастают требования к точности и жесткости передачи, так как увеличивается возможность поломки зубьев вследствие концентрации нагрузки, в особенности при перегрузках.

Дата добавления: 2014-01-07