С помощью системы Эль-Гамаля

Криптосистема Эль-Гамаля

Эта система открытого шифрования предложена Тахер Эль-Гамалем (ElGamal), египетским шифровальщиком в 1985 р.

В отличие от RSA алгоритм Эль-Гамаля не был запатентован и, поэтому, стал более дешевой альтернативой, так как не требовалась оплата взносов за лицензию.

Основана на трудности вычисления дискретных логарифмов в конечном поле.

Организация шифрованной переписки

Пусть пользователь А хочет получить шифрованное сообщение от пользователя В.

Пользователь А должен:

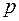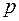1) выбрать простое большое число и найти первообразный корень по модулю (– первообразный корень, есл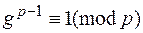и и 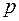не делится на ).

2) выбрать случайное целое число из интервала . Число – закрытый ключ пользователя А;

3) вычислить 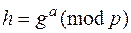. Открытый ключ пользователя А – тройка чисел .

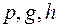4) открытым каналом передать пользователю В открытый ключ

.

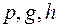Пользователь В должен:

1) выбрать случайным образом рандомизатор – произвольное целое число из отрезка ;

2) разбить свое сообщение на блоки и зашифровать их по формулам

, ;

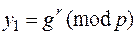3) криптограммой открытого текста 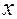есть пара . Ее он отсылает пользователю А.

Чтобы дешифровать криптограмму, пользователь А на своем закрытом ключе вычисляет

.

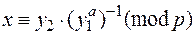Докажем корректность такого шифрования. Так как – первообразный корень по модулю 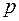, то

.

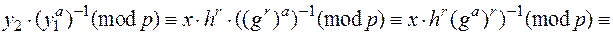
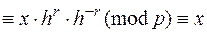Пример 1. Сгенерировать открытый и закрытый ключи для криптосистемы Эль-Гамаля и зашифровать сообщение СКЛО.

Р е ш е н и е. СКЛО = 21 14 15 18. Делим на блоки 2114, 1518, т.е. ,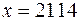

Выберем простое число 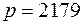, большее, чем блоки. Находим первообразный корень 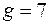по модулю 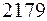(для корня выполнено условие 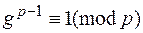). Теперь случайно выберем целое число 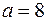из интервала – это закрытый ключ.

.

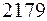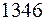(, , ) – открытый ключ. Из отрезка 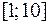выберем рандомизатор 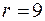и зашифруем:

;

;

.

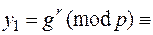
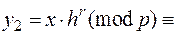
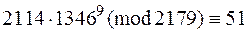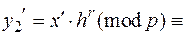
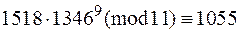Криптограмма 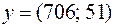и 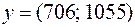. Для дешифрования находим

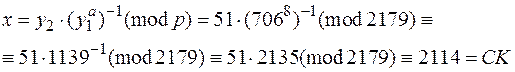
Аналогично =ЛО.

Криптосистему Эль-Гамаля можно использовать в любой конечной группе в мультипликативной группе 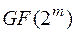характеристики 2 или в группе точек эллиптической кривой над конечным полем.

Алгоритм стал базой для принятия стандартов цифровой подписи: национального стандарта США (DSA) –1994 г. и государственного стандарта Российской федерации ГОСТ Р 34.10. – 1995 г.

Дата добавления: 2014-01-07