Последовательные и параллельные соединения участков электрической цепи

Простейшие соединения элементов электрической цепи – последовательное и параллельное. При последовательном соединении через все элементы течет одинаковый ток. Двухполюсники, образованные последовательным соединением однотипных элементов, и формулы, описывающие эти соединения, показаны на рисунке 4.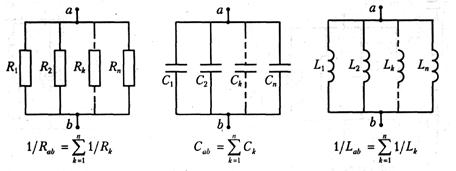

Рисунок 4

Последовательное соединение сопротивлений (рисунок 4, а) можно рассматривать как единое сопротивление R_ab, значение которого равносумме значений отдельных сопротивлений. Последовательное соединение емкостей (рисунок 4, б) представимо единой емкостью С_аЬ, обратное значение которой 1/ С_аb равно сумме обратных значений отдельных емкостей: 1 /C_k. Последовательное соединение индуктивностей (рисунок 4, в), если между ними нет магнитной связи, можно рассматривать как единую индуктивность L_ab. Ее значение равно сумме значений отдельных индуктивностей.

При последовательном соединении элементов напряжение на зажимах U_ab будет равно сумме падений напряжений на отдельных элементах.

При параллельном соединении элементов электрической цепи напряжение на всех элементах одинаково. Такая цепь называется разветвленной электрической цепью. Токи, протекающие через отдельные элементы разветвленной электрической цепи обратно пропорциональны сопротивлениям элементов. Двухполюсники, образованные параллельным соединением однотипных элементов, и формулы, описывающие эти соединения, показаны на рисунке 5.

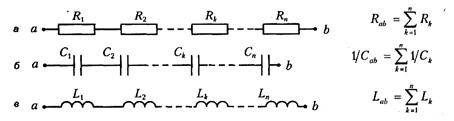
Рисунок 5

Параллельное соединение сопротивлений (рисунок 5, слева) подобно единому сопротивлению R_ab, обратное значение которого 1/ R_ab равно сумме обратных значений отдельных сопротивлений: 1 / R_k. Учитывая, что обратной величиной сопротивления является проводимость, можно констатировать: проводимость параллельного соединения сопротивлений равна сумме их проводимостей.

Параллельное соединение емкостей (рисунок 5, в центре) подобно емкости С_аЬ, значение которой равно сумме значений отдельных емкостей. Параллельное соединение индуктивностей (рисунок 5, справа), если между ними нет магнитной связи, можно рассматривать как единую индуктивность L_ab, обратное значение которой 1 / L_ab равно сумме обратных значений отдельных индуктивностей: 1 / L_k.

ПРИМЕЧАНИЕ

Когда приходится соединять пару очень разных по значению сопротивлений (или индуктивностей), при их последовательном соединении значение общего сопротивления (индуктивности) чуть больше большего, а при параллельном – чуть меньше меньшего из этой пары. Для емкостей ситуация обратная.

Формулы для емкости, образованной последовательным соединением двух емкостей и для сопротивления, образованного двумя параллельно соединенными сопротивлениями, имеют вид:

C_ab = C₁ C₂ / (C₁ + C₂);

R_ab = R₁ R₂ /(R₁ + R₂).

Дата добавления: 2014-01-07