Средняя, среднеквадратичная и наиболее вероятная скорости молекул

Запишем теперь формулы для распределений (2.15) и (2.16) с учетом полученного значения α. Для скоростей вдоль одной из координат (пусть это будет ось х):

(2.19)

Для вектора скорости:

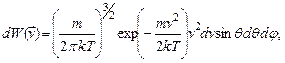(2.20)

где − элемент телесного угла, в который направлен вектор скорости (см. рис. 2.1).

Рис. 2.1.

И, наконец, для абсолютной величины этого вектора:

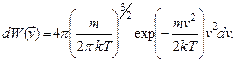(2.21)

Распределения (2.19) - (2.20) называются распределениями Максвелла.

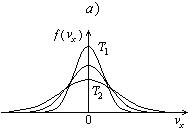
Из (2.21) следует, что функция имеет максимум (см. рис.2.2, б). Этот максимум определяет наиболее вероятную скорость:

(2.22)

Рис. 2.2

При повышении температуры доля быстрых молекул возрастает. Однако в соответствии с условием нормировки (2.14) площадь под кривой остается постоянной и равной единице. В любом случае доля очень быстрых молекул мала: и f (v_x), и r (v) стремятся к нулю при стремлении величины аргумента к бесконечности.

С помощью распределения Максвелла можно найти средние значения разных величин. Для средней скорости молекул получается формула

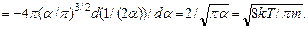(2.23)

Так как то среднеквадратичная скорость с учетом результата (2.17) есть

(2.24)

Как средняя, так и среднеквадратичная скорость лишь ненамного отличаются от наиболее вероятной:

Все эти скорости порядка скорости звука в газе. Для кислорода при комнатной температуре 440 м/c, для водорода она в четыре раза больше.

Средняя энергия поступательного движения молекулы

(2.5).

При комнатной температуре » 3/2×1,38×10^–16×293×10^–7/(1,6×10^–19) = 0,04 эВ, что на два порядка меньше энергии связи атома в молекуле и недостаточно для диссоциации газа.

Дата добавления: 2014-01-07