Комбинаторика

Комбинаторика – раздел математики, изучающий способ построения подмножества некоторого конечного подмножества удовлетворяющее заданным ограничениям.

Подмножество, которое строится называется комбинаторной комбинацией или выборкой.

В комбинаторике есть следующие типы задачи:

1. Подсчет комбинаторных комбинаций (количества подмножеств)

2. Нахождение условий существования определенных комбинаторных комбинаций (конфигураций)

3. Алгоритм построения всех комбинаторных комбинаций удовлетворяющих определённым условиям

4. Нахождение оптимального из комбинаторных конфигураций удовлетворяющих определенным свойствам

Пусть дано множество из 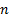элементов 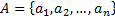(назовем 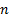– множество). Из этого множества будем формировать различные по длине путем выбора элементов и помещать их в какое-то множество 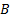. В множестве 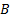некоторые элементы могут повторятся, в этом случае построенное множество 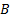будет называться мультимножеством.

Выборкой называется всякое мультимножество с элементами из множества .

Если множество 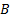состоит их 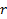элементов, то его называют 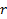– выборкой.

Дата добавления: 2014-01-07