Число упорядоченных выборок без повторения

Пусть дано 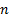– множество . Рассмотрим все подмножества из 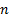– множество , состоящие из 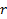элементов. Подмножества не являются мультимножествами. Два подмножества отличающихся порядком элементов считаются разными.

Нас интересуют только упорядоченные подмножества.

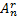– количество упорядоченных выборок объема 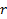без повторений.

Воспользуемся правилом произведения. Первый объект в выборку можно выбрать 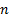способами, второй 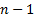способами, …. Нам нужно одновременно выбрать и на 1-ое и на 2-ое и на 3-е и т.д.

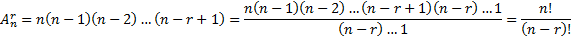
Частным случаем формулы 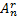является случай, когда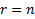 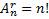. В этом случае каждый раз выбираем 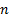элементов в разном порядке, т.е. переставляем 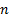элементов на 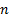местах.

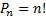– количество перестановок 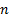элементов на 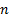местах.

Алгоритмы генерации всех перестановок:

1) Лексикографический порядок

2) Векторы инверсий

3) Вложенные циклы

4) Трансформация смежных элементов

Лексикографический порядок (генерация всех перестановок)

Переставляем элементы конечного множества 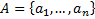, где каждый элемент имеет номер. Поэтому можно переставлять их номера.

При перестановке наборов 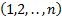считается, что наборы идут в лексикографическом порядке, если числа идут в порядке возрастания.

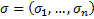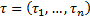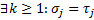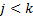Перестановка лексикографически меньше , если и только если для и .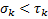

Алгоритм:

Шаг 0:

Записать исходную перестановку и положить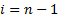

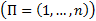
Шаг k:

Вывести на печать перестановку 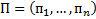и осуществить переход к следующей перестановке следующим образом: Просматривая П справа налево находим самую правую позицию 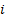, где 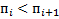, запоминаем 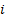. Если 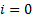, то вычисления прекращают, т.к. все перестановки получены, иначе справа налево находим 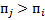получаем промежуточный 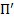, а затем все элементы в 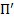переворачиваем и все, 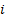становится 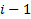и переходим на 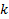-ый шаг.

Дата добавления: 2014-01-07