Различные подходы к отображению моделей процессов

Соответствие между моделью и действительностью: сходство. В предыдущем параграфе мы обсуждали соответствие между моделью и оригиналом с позиций различия между ними. Рассмотрим теперь более трудный вопрос — о сходстве между ними. Поскольку различия между моделью и реальностью принципиально неизбежны и неустра­нимы, существует предел истинности, правильности наших знаний, сконцентрированных в моделях. Является ли этот предел вечным, прин­ципиально неотодвигаемым или имеется возможность неограниченно увеличивать сходство наших моделей с реальностью? Или, говоря фило­софским языком, доступна ли объективная истина субъективному познанию?

Различные философские учения отвечали на этот вопрос по-разному. Субъективные идеалисты вообще отрицали наличие какой-либо реальности вне сознания субъекта либо считали ее продуктом сознания. Античные софисты считали и саму реальность, и всякое знание о внешней реальности относительными, субъективными и индивидуальными; разные мнения об одном, принадлежащие разным субъектам, считались одинаково истинными ("что кому как является, так оно и есть для того, кому является"). Агностики признавали ощущения единственной реаль­ностью и потому считали, что познанию доступны лишь явления, а сущ­ности и закономерности реального мира принципиально непознаваемы. Диалектический материализм освещает этот вопрос в плане отношений между относительной истиной, т.е. объективным, но не полным содержа­нием сегодняшнего человеческого познания, и истиной абсолютной: ис­тина относительная может пополняться, развиваться, приближаясь к истине абсолютной, и принципиального предела этому приближению не существует. Степень правильности относительных истин, наличие в моделях элементов, не обладающих истинностью, обнаруживаются в практике человеческого общества.

Истинность моделей. Весь исторический опыт науки, техники, общественной практики подтверждает верность диалектико-материалистической теории позна­ния. Например, в современной теории тепловых процессов многое со­хранилось со времен С. Карно, но от модели теплорода как особой субстанции — носителя тела пришлось отказаться; в основе современной электродинамики лежат уравнения Максвелла, но от механической максвелловской модели эфира до современных представлений о физичес­ком вакууме — огромная дистанция.

В теории и практике используются различные подходы к отображению моделей процессов. Кратко остановимся на функциональном и объектно-ориентированном подходе. В функциональном подходе главным структурообразующим элементом является функция (действие, операция), в объектно-ориентированном подходе — объект.

Функциональный подход в моделировании процесса сводится к построению схемы процесса в виде последовательности операций, с которыми связаны материальные и информационные объекты, используемые ресурсы, организационные единицы и многое другое. Достоинством функционального подхода является наглядность последовательности и логики операций в процессах предприятия, а недостатком — некоторая субъективность детализации операций.

Объектно-ориентированный подход предполагает вначале выделение объектов, а затем определение тех действий, в которых они участвуют. При этом различают пассивные объекты (материалы, документы, оборудование), над которыми выполняются действия, и активные объекты (организационные единицы, конкретные исполнители, программное обеспечение), которые осуществляют действия. Такой подход позволяет более объективно выделить операции над объектами и решить задачу о целесообразности использования этих объектов. Недостаток объектно-ориентированного подхода заключается в меньшей наглядности конкретных процессов.

§ 4.4. Чёрный ящик

Понятие «чёрный ящик» появилось в связи с попытками описания процесса познания некоторого объекта реального мира, т.е. процесса построения достаточно достоверной модели этого объекта. Рассмотрим такой процесс.

Предположим, есть некоторый объект, обладающий поведением. Это значит, что в него поступают от внешней среды потоки вещества, энергии или сигналов (ВЭ│С), и от него во внешнюю среду поступают другие потоки ВЭ│С. Первые потоки назовём входными сигналами и обозначим буквой Х, вторые – выходными сигналами и обозначим буквой Y. Мы ничего не знаем о том, как этот объект устроен и почему в нём X преобразуется в Y, поэтому он и называется чёрным ящиком на данном этапе познания. Начнём наблюдать за сигналами X и Y, пытаясь уловить связь между их изменениями. Поставим опыты, если мы сами можем изменять входные воздействия, и пронаблюдаем, как при этом будут изменяться выходные сигналы. Собрав достаточно большой объём данных, попытаемся статистически их обработать, и на основе полученной информации построим непротиворечивую гипотезу о внутреннем устройстве исследуемого объекта, на основе которой можно попытаться предсказать поведение объекта. Если дальнейшее поведение объекта не согласуется с данной гипотезой при определённых значениях Х, то гипотеза неверна и подлежит доработки или замене. Если при многократном повторении опытов с объектом гипотеза подтверждается, то признаётся её обоснованность, и гипотеза переходит в разряд теории. Это значит, что мы построили достаточно достоверную модель, т.е. описали поведение объекта таким образом, что стало возможным предсказывать его поведение. Следовательно, его поведение для нас стало в некоторой степени функционированием, которое можно использовать для наших собственных целей, а сам «чёрный ящик» стал для нас уже не таким чёрным, «стенки» его стали прозрачнее. Дальнейшее исследование объекта позволяет уточнять построенную модель, расширять область её применения, распространять её на другие схожие объекты.

Для исследования поведения различных объектов в настоящее время существуют уже достаточно разработанные математические аппараты, такие, как теория компромисса, теория катастрофы, теория хаоса.

§ 5. Классификация систем

Начиная сравнивать и различать системы, считать одни из них одинако­выми, другие — различными, мы тем самым вводим и осуществляем их классификацию.

Важно понять, что классификация - это только модель реальности. Поэтому классификацию не следует абсолютизировать: реальность всегда сложнее любой модели.

Системы можно разделять на классы по различным признакам, и в зависимости от решаемой задачи выбирать разные принципы классификации.

Системы могут быть классифицированы следующим образом:

по виду отображаемого объекта — технические, биологические и др.;

по виду научного направления — математические, физические, химические и пр.;

по виду формализованного аппарата представления системы — детерминированные и стохастические;

по типу целеустремленности — открытые и закрытые;

по происхождению – естественные, искусственные;

по степени организованности — хорошо организованные, плохо организованные (диффузные), самоорганизующиеся системы;

по сложности структуры и поведения — простые и сложные.

Рассмотрим подробно два последних вида классификации систем.

Хорошо организованные системы. Представить анализируемый объект или процесс в виде «хорошо организованной системы» означает определить элементы системы, их взаимосвязь, правила объединения в более крупные компоненты, т.е. определить связи между всеми компонентами и целями системы, с точки зрения которых рассматривается объект или ради достижения которых создается система. Проблемная ситуация может быть описана в виде математического выражения, связывающего цель со средствами, т.е. в виде критерия эффективности, критерия функционирования системы, который может быть представлен сложным уравнением или системой уравнений. Решение задачи при представлении ее в виде хорошо организованной системы осуществляется аналитическими методами формализованного представления системы.

Примеры хорошо организованных систем: солнечная система, описывающая наиболее существенные закономерности движения планет вокруг Солнца; отображение атома в виде планетарной системы, состоящей из ядра и электронов; описание работы сложного электронного устройства с помощью системы уравнений, учитывающей особенности условий его работы (наличие шумов, нестабильности источников питания и т. п.).

Для отображения объекта в виде хорошо организованной системы необходимо выделять существенные и не учитывать относительно несущественные для данной цели рассмотрения компоненты: например, при рассмотрении солнечной системы не учитывать метеориты, астероиды и другие мелкие по сравнению с планетами элементы межпланетного пространства.

Описание объекта в виде хорошо организованной системы применяется в тех случаях, когда можно предложить детерминированное описание и экспериментально доказать правомерность его применения, адекватность модели реальному процессу. Попытки применить класс хорошо организованных систем для представления сложных многокомпонентных объектов или многокритериальных задач плохо удаются: они требуют недопустимо больших затрат времени, практически нереализуемы и неадекватны применяемым моделям.

Плохо организованные системы. При представлении объекта в виде «плохо организованной или диффузной системы» не ставится задача определить все учитываемые компоненты, их свойства и связи между ними и целями системы. Система характеризуется некоторым набором макропараметров и закономерностями, которые находятся на основе исследования не всего объекта или класса явлений, а на основе определенной с помощью некоторых правил выборки компонентов, характеризующих исследуемый объект или процесс. На основе такого выборочного исследования получают характеристики или закономерности (статистические, экономические) и распространяют их на всю систему в целом. При этом делаются соответствующие оговорки. Например, при получении статистических закономерностей их распространяют на поведение всей системы с некоторой доверительной вероятностью.

Подход к отображению объектов в виде диффузных систем широко применяется при: описании систем массового обслуживания, определении численности штатов на предприятиях и учреждениях, исследовании документальных потоков информации в системах управления и т. д.

Самоорганизующиеся системы. Отображение объекта в виде самоорганизующейся системы — это подход, позволяющий исследовать наименее изученные объекты и процессы. Самоорганизующиеся системы обладают признаками диффузных систем: стохастичностью поведения, нестационарностью отдельных параметров и процессов. К этому добавляются такие признаки, как:

- непредсказуемость поведения;

- способность адаптироваться к изменяющимся условиям среды, изменять структуру при взаимодействии системы со средой, сохраняя при этом свойства целостности;

- способность формировать возможные варианты поведения и выбирать из них наилучший

- и др.

Иногда этот класс разбивают на подклассы, выделяя адаптивные или самоприспосабливающиеся системы, самовосстанавливающиеся, самовоспроизводящиеся и другие подклассы, соответствующие различным свойствам развивающихся систем.

Примеры: биологические организации, коллективное поведение людей, организация управления на уровне предприятия отрасли, государства в целом, т.е. в тех системах, где обязательно имеется человеческий фактор.

При применении отображения объекта в виде самоорганизующейся системы задачи определения целей и выбора средств как правило, разделяются. При этом задача выбора целей может быть, в свою очередь, описана в виде самоорганизующейся системы, т.е. структура функциональной части АСУ, структура целей плана может разбиваться так же, как и структура обеспечивающей части АСУ (комплекс технических средств АСУ) или организационная структура системы управления.

Большинство примеров применения системного анализа основано нa представлении объектов в виде самоорганизующихся систем.

Определение большой системы. Существует ряд подходов к разделению систем по сложности. В частности, Г. Н. Поваров в зависимости от числа элементов, входящих в систему, выделяет четыре класса систем: малые системы (10…10³ элементов); сложные (10⁴…10⁷ элементов); ультрасложные (10⁷…10³⁰ элементов); суперсистемы (10³⁰…10²⁰⁰ элементов). Так как понятие элемента возникает относительно задачи и цели исследования системы, то и данное определение сложности явится относительным, а не абсолютным.

Английский кибернетик С. Бир классифицирует все кибернетические системы на простые и сложные в зависимости от способа описания: детерминированного или теоретико-вероятностного. А. И. Берг определяет сложную систему как систему, которую можно описать не менее чем на двух различных математических языках (например, с помощью теории дифференциальных уравнений и алгебры Буля).

Очень часто сложными системами называют системы, которые нельзя корректно описать математически, либо потому что в системе имеется очень большое число элементов, неизвестным образом связанных друг с другом, либо неизвестна природа явлении, протекающих в системе. Все это свидетельствует об отсутствии единого определения сложности системы.

При разработке сложных систем возникают проблемы, относящиеся не только к свойствам их составляющих элементов и подсистем, но также к закономерностям функционирования системы в целом. При этом появляется широкий круг специфических задач, таких, как определение общей структуры системы, организация взаимодействия между элементами и подсистемами; учет влияния внешней среды; выбор оптимальных режимов функционирования системы; оптимальное управление системой и др.

Чем сложнее система, тем большее внимание уделяется этим вопросам. Математической базой исследования сложных систем является теория систем. В теории систем большой системой (сложной, системой большого масштаба, Large Scale Systems) называют систему, если она состоит из большого числа взаимосвязанных и взаимодействующих между собой элементов и способна выполнять сложную функцию.

Четкой границы, отделяющей простые системы от больших, нет. Деление это условное и возникло из-за появления систем, имеющих в своем составе совокупность подсистем с наличием функциональной избыточности. Простая система может находиться только в двух состояниях: состоянии работоспособности (исправном) и состоянии отказа (неисправном). При отказе элемента простая система либо полностью прекращает выполнение своей функции, либо продолжает ее выполнение в полном объеме, если отказавший элемент резервирован. Большая система при отказе отдельных элементов и даже целых подсистем не всегда теряет работоспособность, зачастую только снижаются характеристики ее эффективности. Это свойство больших систем обусловлено их функциональной избыточностью и, в свою очередь, затрудняет формулировку понятия «отказ» системы.

Под большой системой понимается совокупность материальных ресурсов, средств сбора, передачи и обработки информации, людей-операторов, занятых на обслуживании этих средств, и людей-руководителей, облеченных надлежащими правами и ответственностью для принятия решений. Материальные ресурсы — это сырье, материалы, полуфабрикаты, денежные средства, различные виды энергии, станки, оборудование, люди, занятые на выпуске продукции, и т. д. Все указанные элементы ресурсов объединены с помощью некоторой системы связей, которые по заданным правилам определяют процесс взаимодействия между элементами для достижения общей цели или группы целей.

Примеры больших систем: информационная система; пассажирский транспорт крупного города; производственный процесс; система управления полетом крупного аэродрома; энергетическая система и др.

§6. Декомпозиция сложных объектов (разделение на элементы на примере ТС)

В основу декомпозиции системы положен принцип выделения и рассмотрения структур с двухуровневой иерархией: ТО разделяют на несколько элементов, каждый из которых имеет свою определённую функцию (или несколько функций) по обеспечению работы ТО. Сам технический объект представляет верхний уровень, а выделенные функциональные элементы – нижний.

При углублении анализа каждый выделенный элемент рассматривается как самостоятельный ТО, который также разделяется на несколько функциональных элементов и т.д. Объединение таких двухуровневых структур позволяет получить многоуровневую иерархическую структуру.

Главный момент в этом процессе – выделение двухуровневой структуры.

Предельное разделение ТО на элементы возможно до неделимых в функциональном смысле элементов (например, шарик в подшипнике).

Определение 1. Базовым (неделимым) элементом называется деталь (или часть детали, или совокупность частей деталей) с минимальным числом функций по обеспечению работы других элементов системы, при любом делении которых появляются элементы, не имеющие самостоятельной функции или с одинаковыми функциями.

Одновременно с разделением ТО на элементы выделяют объекты окружающей среды, с которыми рассматриваемый ТО находится в функциональном или вынужденном взаимодействии и которые существенно влияют на конструкцию ТО. К таким объектам в первую очередь относят объекты, воспринимающие действие ТО (компонента G в описании потребности P=(D,G,H)). Также к таким объектам окружающей среды относятся подводимая энергия, управляющие сигналы, неблагоприятные излучения и другие воздействия, оказывающие существенное влияние на конструкцию ТО.

При декомпозиции ТО также большое внимание уделяется главным элементам.

Определение 2. К главным элементам относятся рабочие органы и другие элементы, которые непосредственно взаимодействуют с предметом обработки G и другими объектами окружающей среды.

Свойства главных элементов.

1. функция главного элемента совпадает с функцией ТО или в решающей мере зависит от последней;

2. объекты ОС для главного элемента, как правило, совпадают с объектами, на которые направлено действие ТО.

Пример.

ТО – ручка для письма, G – бумага, главный элемент – перо или шариковый узел. Функция главного элемента – образование на бумаге видимого следа – совпадает с функцией объекта.

§ 7. Оптимизация

§ 7.1. Терминология задач оптимизации

Если некоторое действие или цепочку целенаправленных действий можно произвести различными способами, то возникает вопрос о выборе единственного решения из множества решений. Решения, по тем или другим признакам предпочтительные перед другими, называются оптимальными, а сама операция предпочтения – оптимизацией. Постановка задач оптимизации рассматривается наукой «Исследование операций» (ИСО). Воспользуемся терминами ИСО для постановки задачи оптимизации.

Операцией называется всякое мероприятие (система действий), объединенное единым замыслом и направленное к достижению определённой цели.

Операция есть всегда управляемое мероприятие. От нас зависит ход и исход операции, т.е. каким способом выбрать некоторые параметры, характеризующие её организацию. «Организация» здесь понимается в широком смысле слова, включая набор технических средств, применяемых в операции.

Всякий определенный выбор зависящих от нас параметров называется решением.

Те параметры, совокупность которых образует решение, называются элементами решения. В качестве элементов решения могут фигурировать различные числа, векторы, функции, физические признаки и т. д.

Пример. Если составляется план перевозок однородных грузов из пунктов отправления А₁, А₂,..., А_m, в пункты назначения В₁, В₂, …, В_n, то элементами решения будут числа х_ij показывающие, какое количество груза будет отправлено из i -го пункта отправления A_i в j -и пункт назначения В_j. Совокупность чисел x₁₁,x₁₂,…,x_1n,…,x_i1,x_i2,…,x_in,…,x_m1,x_m2,…, x_mn образует решение.

Для упрощения мы будем всю совокупность элементов решения обозначать одной буквой х и говорить «решение х». В своей совокупности они в свою очередь формируют так называемое «множество возможных решений». Обозначим это множество буквой X, а тот факт, что решение х принадлежит этому множеству, будем записывать в виде формулы: х Î Х.

Кроме элементов решения, которыми мы, в каких-то пределах, можем распоряжаться, в любой задаче исследования операций имеются еще и заданные, «дисциплинирующие» условия, которые фиксированы с самого начала и нарушены быть не могут (например, грузоподъемность машины; размер планового задания и т. п.). В частности, к таким условиям относятся средства (материальные, технические, людские), которыми мы вправе распоряжаться. Это ограничения, налагаемые на решение. Обозначим совокупность таких ограничений одной буквой a.

Чтобы сравнивать между собой по эффективности разные решения, нужно иметь некоторый количественный критерий, так называемый показатель эффективности W (его часто называют «целевой функцией»). Этот показатель выбирается так, чтобы он отражал целевую направленность операции. «Лучшим» будет считаться то решение, которое в максимальной степени способствует достижению поставленной цели. Чтобы выбрать, «назвать по имени» показатель эффективности W, нужно прежде всего спросить себя: чего мы хотим, к чему стремимся, предпринимая операцию? Выбирая решение, мы, естественно, предпочтем такое, которое обращает показатель эффективности W в максимум (или в минимум). Например, доход от операции хотелось бы обратить в максимум; если же показателем эффективности являются затраты, их желательно обратить в минимум. Если показатель эффективности желательно максимизировать, мы это будем записывать в виде W ® max, а если минимизировать — W ® min.

§ 7.2. Прямые и обратные задачи оптимизации

Задачи исследования операций делятся на две категории: прямые и обратные.

Прямые задачи отвечают на вопрос: «Что будет, если...?» Что будет, если в заданных условиях мы примем некоторое решение х Î X? В частности, чему будет равен, при данном решении х, выбранный показатель эффективности W? Для решения такой задачи строится математическая модель, позволяющая выразить один или несколько показателей эффективности через заданные условия и элементы решения.

Обратные задачи отвечают на вопрос: «Как сделать, чтобы…?» Как выбрать решение х для того, чтобы показатель эффективности W обратился в максимум?

Очевидно, что прямые задачи проще обратных и что для решения обратной задачи прежде всего надо уметь решать прямую. Для некоторых типов операций прямая задача решается настолько просто, что ею специально не занимаются. Для других типов операций построение математических моделей и вычисление показателя эффективности само по себе далеко не тривиально. Обратная задача и есть задача оптимизации.

§ 7.3. Постановка задачи оптимизации (обратной задачи ИСО) в общей форме.

Пусть есть некоторая операция 0, на успех которой мы можем влиять, выбирая тем или другим способом решение х (вспомним, что х — не число, а целая группа параметров). Пусть эффективность операции характеризуется одним показателем W ® max.

Пусть все условия операции полностью известны заранее, не содержат неопределенности. Тогда все факторы, от которых зависит успех операции, - это зависящие от нас элементы решения, образующие в своей совокупности решение х.

Показатель эффективности W зависит от элементов решения и от ограничивающих факторов. Это мы запишем в виде формулы:

W=W(a,x) (1)

Будем считать, что вид зависимости (1) нам известен, т. е. прямая задача решена. Тогда обратная задача формулируется следующим образом:

Найти такое решение х = х*, которое обращает показатель эффективности W в экстремум, например, в максимум. W* = max {W (a, х)}. (2)

xÎX

Формула (2) читается так: W* есть максимальное значение W(х), взятое по всем решениям, входящим в множество возможных решений X.

Если число возможных вариантов решения, образующих множество X, невелико, то можно попросту вычислить величину W для каждого из них, сравнить между собой полученные значения и непосредственно указать один или несколько оптимальных вариантов, для которых W достигает максимума. Такой способ нахождения оптимального решения называется «простым перебором». Однако, когда число возможных вариантов решения, образующих множество X, велико, поиск среди них оптимального «вслепую», простым перебором, затруднителен, а зачастую практически невозможен. В этих случаях применяются методы «направленного перебора», обладающие той общей особенностью, что оптимальное решение находится рядом последовательных «попыток» или «приближений», из которых каждое последующее приближает нас к искомому оптимальному.

Существует целый набор численных методов отыскания экстремумов, некоторые из них включают элемент «случайного поиска», который для многомерных задач нередко оказывается эффективнее упорядоченного перебора.

§ 7.4. Задачи линейного программирования

Рассмотрим простейший случай: выбор показателя эффективности W явно диктуется целевой направленностью операции, а ее условия известны заранее (детерминированная задача). В этом случае показатель эффективности зависит только от двух групп параметров: заданных условий a и элементов решения х. Т. е. W = W{ a ,x).

Пусть решение х представляет собой n-мерный вектор:

х = (х₁, х₂,..., x_n), где х_i – элементы решения

Требуется найти такие значения х₁, х₂,..., x_n, которые обращают величину W в экстремум.

Трудности, возникающие при решении задач математического программирования, зависят:

а) от вида функциональной зависимости, связывающей W с элементами решения,

б) от «размерности» задачи, т. е. от количества элементов решения х₁, х₂,..., x_n и

в) от вида и количества ограничений, наложенных на элементы решения.

Среди задач математического программирования самыми простыми (и лучше всего изученными) являются так называемые задачи линейного программирования. Характерно для них то, что:

а) показатель эффективности (целевая функция) W линейно зависит от элементов решения х₁, х₂,..., x_n и

б) ограничения, налагаемые на элементы решения, имеют вид линейных равенств или неравенств относительно х₁, х₂,..., x_n.

Линейные зависимости часто встречаются на практике. Приведем несколько примеров задач линейного программирования.

1. Задача о пищевом рационе.

Ферма производит откорм скота с коммерческой целью. Для простоты допустим, что имеется всего четыре вида продуктов: П₁, П₂, П₃, П₄. Стоимость единицы каждого продукта равна соответственно c₁, c₂, c₃, c₄. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков — не менее b₁ единиц; углеводов— не менее b₂ единиц; жиров — не менее b₃ единиц. Для продуктов П₁, П₂, П₃, П₄ содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и задано таблицей

Элементы Продукты	Белки	Углеводы	Жиры
П1	a11	a12	a13
П2	a21	a22	a23
П3	a31	a32	a33
П4	a41	a42	a43

где a_ij (i = 1, 2, 3, 4; j = 1, 2, 3) — некоторые определенные числа; первый индекс указывает номер продукта, второй — номер элемента (белки, углеводы, жиры). Требуется составить такой пищевой рацион (т. е. назначить количества продуктов П₁, П₂, П₃, П₄, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.

Составим математическую модель. Обозначим через x₁, x₂, x₃, x₄ количества продуктов П₁, П₂, П₃, П₄, входящих в рацион. Показатель эффективности, который требуется минимизировать, — стоимость рациона (обозначим её L ); она линейно зависит от элементов решения x₁, x₂, x₃, x₄: L = c₁ x₁ + c₂ x₂ + c₃ x₃ + c₄ x_{4. .}

Итак, вид целевой функции известен и она линейна. Запишем теперь в виде формул ограничительные условия по белкам, углеводам и жирам: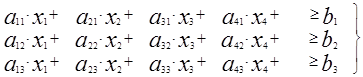

Эти линейные неравенства представляют собой ограничения, налагаемые на элементы решения x₁, x₂, x₃, x₄. Таким образом, поставленная задача сводится к следующей: найти такие неотрицательные значения переменных x₁, x₂, x₃, x_4, чтобы они удовлетворяли ограничениям — неравенствам и одновременно обращали в минимум линейную функцию этих переменных: L = c₁ x₁ + c₂ x₂ + c₃ x₃ + c₄ x₄ ® min

2. Задача о планировании производства.

Предприятие производит изделия трех видов: И₁, И₂, И₃. По каждому виду изделия предприятию спущен план, по которому оно обязано выпустить не менее b₁ единиц изделия И₁, не менее b₂ единиц изделия И₂ и не менее b₃ единиц изделия И₃. План может быть перевыполнен, но в определенных границах; условия спроса ограничивают количества произведенных единиц каждого типа: не более соответственно b₁, b₂, b₃ единиц. На изготовление изделий идет какое-то сырье; всего имеется четыре вида сырья: S₁, S₂, S₃, S₄, причем запасы ограничены числами g₁, g₂, g₃, g₄ единиц каждого вида сырья. Теперь надо указать, какое количество сырья каждого вида идет на изготовление каждого вида изделий. Обозначим a_{i j} количество единиц сырья вида S_j (j = 1,2,3,4), потребное на изготовление одной единицы изделия И_i, (i = 1, 2, 3). Первый индекс у числа a_{i j} — вид изделия, второй — вид сырья. Значения a_{i j} сведены в матрицу.

Сырьё Изделия	S1	S2	S3	S4
И1	a11	a12	a13	a14
И2	a21	a22	a23	a24
И3	a31	a32	a33	a34

При реализации одно изделие И_i приносит предприятию прибыль c_i. Требуется так спланировать производство (сколько каких изделий производить), чтобы план был выполнен или перевыполнен (но при отсутствии «затоваривания»), а суммарная прибыль обращалась в максимум.

Запишем задачу в форме ЗЛП.

Элементами решения будут x₁, x₂, x₃ – количества единиц изделий U₁, U₂, U₃, которые мы произведём.

Запишем условия – ограничения.

Обязательность выполнения плана:

Отсутствие затоваривания: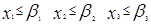

Нам должно хватить сырья: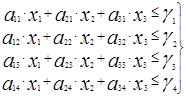

Теперь целевая функция: прибыль, приносимая планом

L = c₁ x₁ + c₂ x₂ + c₃ x₃ ® max

Таким образом, мы снова получили ЗЛП.

3. Задача о загрузке оборудования.

Ткацкая фабрика располагает двумя видами станков, изних N₁ станков типа 1 и N₂ станков типа 2. Станки могут производить три вида тканей: Т₁, Т₂, Тз, но с разной производительностью. Данные a_ij производительности станков даны в таблице (первый индекс — тип станка, второй — вид ткани).

Ткань Станок	T1	T2	T3
	a11	a12	a13
	a21	a22	a23

Каждый метр ткани вида T₁ приносит фабрике доход c₁, вида Т₂ — доход c₂, Т₃ — доход с₃. Фабрике предписан план, согласно которому она должна производить в месяц не менее b₁ метров ткани Т₁, b₂ метров ткани Т₂, b₃ метров ткани Т_3. Количество метров каждого вида ткани не должно превышать соответственно b₁, b₂, b₃ метров. Кроме того, все без исключения станки должны быть загружены. Требуется так распределить загрузку станков производством тканей Т₁, Т₂, Т₃, чтобы суммарный месячный доход был максимален.

На первый (легкомысленный) взгляд эта задача - родная сестра предыдущей. Но если мы примем за x₁, x₂, x₃ количества тканей трёх видов, то не сможем учесть возможности оборудования. Что же здесь является элементами решения? Возможно, количество станков 1 и 2 вида, занятыми производством тканей каждого вида. Для удобства обозначим элементы решения буквами x с двумя индексами: первый – тип станка, второй - вид ткани. Всего будет шесть элементов решения

x₁₁ x₁₂ x₁₃

x₂₁ x₂₂ x₂₃

Здесь x_ij -количество станков i– ого вида, занятых изготовлением ткани j– ого вида.

Запишем условия-ограничения.

Все станки должны быть задействованы: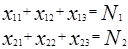

Обеспечим выполнение плана:

Ограничим перевыполнение плана: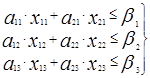

Запишем суммарный доход от производства всех видов тканей. Суммарное количество метров ткани Т₁, произведённое всеми станками, равно a₁₁ × x₁₁ + a₂₁ × x₂₁, и принесёт доход c₁×(a₁₁ ×x₁₁ + a₂₁ ×x₂₁). Суммарный доход равен

L = c₁×(a₁₁ ×x₁₁ + a₂₁ ×x₂₁) + c₂ (a₁₂ ×x₁₂ + a₂₂ ×x₂₂) + c₃ (a₁₃ ×x₁₃ + a₂₃ ×x₂₃) ® max

4. Задача о снабжении сырьем.

Имеются три промышленных предприятия: П₁, П₂, П₃, требующих снабжения определенным видом сырья. Потребности в сырье каждого предприятия равны соответственно a₁, a₂, a₃ единиц. Имеются пять сырьевых баз, расположенных от предприятий на каких-то расстояниях и связанных с ними путями сообщения с разными тарифами. Единица сырья, получаемая предприятием П_i, с базы Б_j обходится предприятию в c_{i j} рублей (первый индекс — номер предприятия, второй — номер базы)

Базы Предприятия	Б1	Б2	Б3	Б4	Б5
П1	с11	с12	с13	с14	с15
П2	с21	с22	с23	с24	с25
П3	с31	с32	с33	с34	с35

Возможности снабжения сырьем с каждой базы ограничены ее производственной мощностью: b₁, b₂, b₃, b₄, b₅ единиц сырья. Требуется составить такой план снабжения предприятий сырьем (с какой базы, куда и какое количество сырья везти), чтобы потребности предприятий были обеспечены при минимальных расходах на сырье.

Поставим задачу линейного программирования. Обозначим x_ij количество сырья, получаемого i- ым предприятием c j- ой базы. Всего план будет состоять из 15 элементов решения:

Введём ограничения по потребностям. Они состоят в том, что каждое предприятие получит нужное ему количество сырья (ровно столько, сколько ему нужно):

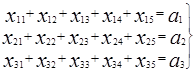
Теперь запишем ограничения-неравенства, вытекающие из производственных мощностей баз: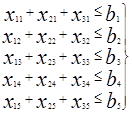

Запишем суммарные расходы на сырьё, которые мы хотим минимизировать. С учётом данных таблицы тарифов получим .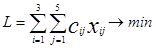

§ 7.5. Основная задача линейного программирования

Существует стандартная форма задачи линейного программирования, так называемая «основная задача линейного программирования» (ОЗЛП), которая формулируется так: найти неотрицательные значения переменных х₁, х₂,..., x_n, которые удовлетворяли бы условиям-равенствам

(3)

и обращали бы в максимум линейную функциюэтихпеременных:

L = c₁ x₁ + c₂ x₂ +…+ c_n x_n ® max. (4)

Любую задачу линейного программирования можно свести к ОЗЛП.

Возможен и обратный переход: от ОЗЛП к задаче с ограничениями-неравенствами.

Назовём допустимым решением ОЗЛП всякую совокупность неотрицательных значений х₁, х₂,..., x_n,, удовлетворяющую условиям (3). Оптимальным назовём то из допустимых решений, которое обращает в максимум функция (4).

Это решение существует не всегда.

Во-первых, может оказаться, что уравнения (3) несовместны (противоречат друг другу).

Во-вторых, может оказаться, что они совместны, но не в области неотрицательных значений.

В-третьих, может быть и так, наконец, что допустимые решения ОЗЛП существуют, но среди них нет оптимальных, т.к. функция L в ОДР не ограничена сверху.

§ 7.6. Геометрическая интерпретация ОЗЛП

Пусть имеется m условий – равенств (3). Предположим для простоты, что все они линейно независимы. Пусть также число линейно независимых уравнений m на 2 меньше числа переменных n (n-m=k=2). Именно такой частный случай даёт возможность геометрической интерпретации на плоскости.

Мы знаем, что m линейно независимых уравнений всегда можно разрешить для m базисных переменных, выразив их через остальные свободные, число которых равно в примере n-m=k=2.

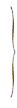Предположим, что свободные переменные x₁ и x₂, а остальные x₃, x₄,…x_n – базисные. Тогда вместо m уравнений (3) получают m уравнений, разрешаемых относительно x₃, x₄,…x_n.

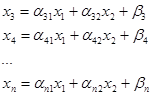
(5)

Рассмотрим плоскость х₁Ох₂. Поскольку х₁ и х₂ должны быть больше или равны 0, то допустимые значения свободных переменных выше оси Ох₁ и правее оси Ох₂. Покажем это штриховкой.

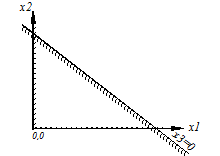
Построим на плоскости х₁Ох₂ область допустимых решений (ОДР) или убедимся, что её не существует. Базисные переменные x₃, x₄,…x_n должны быть неотрицательны и удовлетворять условиям (5). Положим в первом уравнении (5) x₃=0 и получим уравнение прямой линии 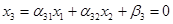. На этой прямой линии x₃=0. По одну сторону от неё x₃>0, по другую x₃<0. Пусть положительная сторона оказалась ниже и левее прямой x₃=0. Покажем это штриховкой.

Аналогично поступим и со всеми остальными условиями (5).

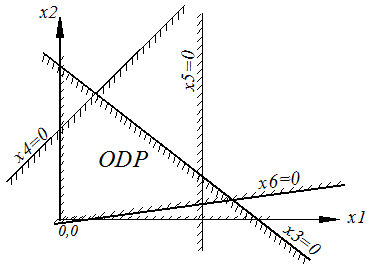
Каждое из них изображается прямой со штриховкой, указывающей «допустимую» полуплоскость, где только и может лежать решение.

Мы построим n прямых: две оси и n –2 прямых x₃=0, x₄=0, …, x_n=0. Каждая из них определяет «допустимую» полуплоскость. Часть первого квадранта, принадлежащая одновременно всем этим полуплоскостям, и есть область допустимых решений.

Может оказаться, что ОДР не существует, а значит, уравнения (5) несовместны в области неотрицательных значений переменных или вообще несовместны. Также может оказаться, что ОДР существует, но не замкнута.

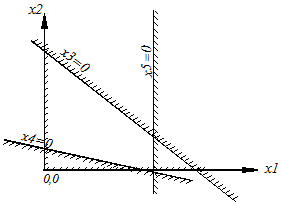
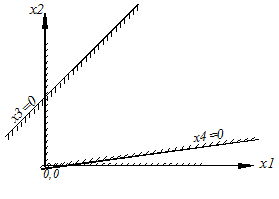
Предположим, что ОДР существует, замкнута и мы её построили. Она представляет собой неправильный многоугольник. Как найти оптимальное решение среди решений из этой области?

Для этого дадим геометрическую интерпретацию (4) L ® max. Подставив выражения (5) в (4) выразим L через свободные переменные х₁ и х₂. После приведения подобных членов получим

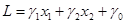(6)

Отбросим свободный член g₀, т.к. максимум функции L достигается при тех же значениях, что и максимум функции

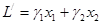(7)

Изобразим геометрически условие L^’ ® max. Положим сначала L^’=0, т.е. g₁x₁+g₂x₂=0 и построим на плоскости прямую с таким уравнением; она проходит через начало координат.

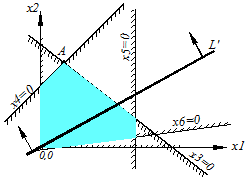
Назовём её опорной прямой. Если будем придавать некоторые значения С₁, С₂, С₃, …, прямая будет перемещаться параллельно самой себе. При перемещении в одну сторону L^’ будет возрастать, в другую – убывать. Отметим на чертеже стрелками направление, в котором L^’ возрастает. L^’ достигает максимума в точке А, крайней точке ОДР в направлении стрелок. В этой точке свободные переменные принимают оптимальное значение x₁^* и x₂^*. Из них по (5) можно найти оптимальные значения других, базисных переменных x₃^*, x₄^*,… x_n^*. Максимум достигается в одной из вершин ОДР, где по крайней мере две базисные переменные (х₃ и х₄) равны нулю.

Если ОДР не ограничена сверху, то оптимального решения на существует. В разумно поставленных задачах такого недоразумения не возникает.

Также может быть, что оптимальное решение есть, но оно не единственное, их бесконечное множество. Максимум достигается на отрезке АВ, параллельном опорной прямой, т.е. и в вершине А, и в вершине В. т.е. и в этом случае можно ограничиться поиском в вершинах.

Итак, оптимальное решение, если оно существует, всегда достигается в одной из вершин ОДР, в точке, где по крайней мере k (k=n-m) из переменных x₃, x₄,…x_n равны нулю, а остальные неотрицательны. Это правило справедливо для любого k. Если k = 3, то ОДР представляет собой многогранник в трёхмерном пространстве. Если k > 3, то задача теряет наглядность, а ОДР является тогда гипер - многогранником в многомерном (4 и более) пространстве.

§ 8. Многокритериальная оптимизация.

Мы до сих пор рассматривали только самые простые случаи, когда ясен критерий, по которому производится оценка эффективности, и требуется обратить в максимум (минимум) один-единственный показатель W. К сожалению, на практике такие задачи, где единственный критерий оценки однозначно диктуется целевой направленностью операции, встречаются не так уж часто — преимущественно при рассмотрении небольших по масштабу и скромных по значению мероприятий. А когда идет речь о крупномасштабных, сложных операциях, затрагивающих разнообразные интересы их организаторов и общества в целом, то их эффективность, как правило, не может быть полностью охарактеризована с помощью одного-единственного показателя эффективности W. На помощь ему приходится привлекать другие, дополнительные. Такие задачи исследования операций называются многокритериальными.

Рассмотрим пример такой задачи. Организуется оборона важного объекта от воздушных налетов. В нашем распоряжении — какие-то средства противовоздушной обороны, которые надо разумным образом разместить вокруг объекта, организовать их взаимодействие, распределить между ними цели, назначить боезапас и т. д. Допустим, что каждый из самолетов противника, участвующих в налете, является потенциальным носителем мощного поражающего средства, которое, будучи применено по объекту, гарантирует его уничтожение. Тогда главная задача операции — не допустить к объекту ни одного самолета, а естественный показатель эффективности — вероятность W того, что ни один самолет не прорвется к объекту. Но единственный ли это важный для нас показатель? Безусловно, нет. При одной и той же вероятности W мы предпочтем все-таки решение, при котором будет погибать в среднем побольше самолетов противника. Отсюда второй показатель эффективности М — среднее число пораженных целей, который нам тоже хотелось бы максимизировать. Кроме того, нам далеко не все равно, каковы будут наши собственные боевые потери П — еще один критерий, который хотелось бы минимизировать. Желательно было бы, кроме того, сделать поменьше средний расход боеприпасов R, и т. д.

Другой пример — на этот раз из совершенно мирной области. Организуется (или реорганизуется) работа промышленного предприятия. Под углом зрения какого критерия надо выбирать решение? С одной стороны, нам хотелось бы обратить в максимум валовой объем продукции V. Желательно также было бы получить максимальный чистый доход D. Что касается себестоимости S, то ее хотелось бы обратить в минимум, а производительность труда П — в максимум. При обдумывании задачи может возникнуть еще ряд дополнительных критериев.

Такая множественность показателей эффективности, из которых одни желательно обратить в максимум а другие — в минимум, характерна для любой сколько-нибудь сложной задачи, требующей оптимизации.

Итак, типичной для крупномасштабной задачи исследования операций является многокритериальность — наличие ряда количественных показателей W₁, W₂..., одни из которых желательно обратить в максимум, другие — в минимум.

Спрашивается, можно ли найти решение, одновременно удовлетворяющее всем этим требованиям? Со всей откровенностью ответим: нет. Решение, обращающее в максимум один какой-то показатель, как правило, не обращает ни в максимум, ни в минимум другие.

Как же решаются такие задачи? Возможно, есть способы сведения многокритериальных задач к однокритериальным? Да, такие способы есть, хотя их использование привносит в задачи значительную субъективность.

1) Нередко применяется следующий способ составления «обобщенного показателя эффективности». Он представляет собой «взвешенную сумму» частных показателей, в которую каждый из них W_i, входит с каким-то «весом» d_i, отражающим его важность:

W = d₁ W₁ + d₂ W₂ +... (1)

Для тех показателей, которые желательно увеличить, веса берутся положительными, уменьшить — отрицательными.

При произвольном назначении весов d_i этот способ не приводит к сколько-нибудь достоверным результатам. Но если оценку весовым коэффициентам даёт опытный эксперт (а лучше, группа экспертов, и их независимые оценки усредняются), то можно говорить об определённой приближённости модели к реальности.

2) Существует ещё один, часто применяемый способ свести многокритериальную задачу к однокритериальной — это выделить один (главный) показатель W_гл и стремиться его обратить в максимум (минимум), а на все остальные W₁, W₂, … наложить только некоторые ограничения, потребовав, чтобы они были не меньше каких-то заданных величин. Например, при оптимизации плана работы предприятия можно потребовать, чтобы прибыль была максимальна, план по ассортименту — выполнен или перевыполнен, а себестоимость продукции — не выше заданной. При таком подходе все показатели, кроме одного — главного, переводятся в разряд заданных условий a.

Существуют способы осмыслить решение многокритериальных задач, не прибегая к свёртке или замене критериев.

3) Математический аппарат не панацея, и не следует слепо доверять рекомендациям математических выкладок. Но он помогает «выбраковать» из множества возможных решений Х заведомо неудачные, уступающие другим по всем критериям.

Проиллюстрируем прием выделения таких решений на примере задачи с двумя критериями: W₁ и W₂ (оба требуется максимизировать). Множество Х состоит из конечного числа n возможных решений х₁, x₂, … x_n. Каждому решению соответствуют определенные значения показателей W₁, W₂. Будем изображать решение точкой на плоскости с координатами W₁, W₂ и занумеруем точки соответственно номеру решения (рис).

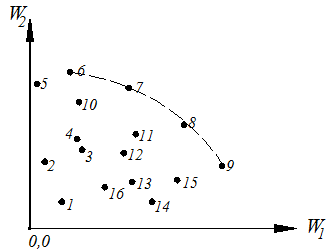
Пусть в составе множества возможных решений есть два решения х₁ и х₃ такие, что оба критерия W₁ и W₂ для третьего решения больше или равны соответствующим критериям для первого решения, причем хотя бы один из них действительно больше. Очевидно, тогда в составе множества Х нет смысла сохранять решение х₁, оно вытесняется (или, как говорят, «доминируется») решением х₃. Ладно, выбросим решение x₁ как неконкурентоспособное и перейдем к сравнению других решений по всем критериям. В результате такой процедуры отбрасывания заведомо непригодных, невыгодных решений множество Х обычно сильно уменьшается: в нем сохраняются только так называемые эффективные решения, характерные тем, что ни для одного из них не существует доминирующего решения. Эти решения образуют так называемое множество несравнимых вариантов, множество парето.

В примере из всего множества Х эффективными будут только решения х₆, x₇, x₈, x₉, лежащие на правой верхней границе области возможных решений (см. точки, соединенные пунктиром, на рис). Для всякого другого решения существует хотя бы одно доминирующее, для которого либо W₁, либо W₂, либо оба больше, чем для данного. И только для решений, лежащих на правой верхней границе, доминирующих не существует.

Когда из множества возможных решений выделены эффективные, «переговоры» могут вестись уже в пределах этого «паретовского» множества. В примере решение х₆ — наилучшее по критерию W₂, x₉ — по критерию W₁. Дело лица, принимающего решение, выбрать тот вариант, который для него предпочтителен и «приемлем» по обоим критериям. (Болото парето, стоячая волна здравого смысла)

Аналогично строится множество эффективных решений и в случае, когда показателей не два, а больше. При числе их, большем трех, геометрическая интерпретация теряет наглядность, но суть дела сохраняется. Множество эффективных решений легче обозримо, чем полное множество X. Что касается окончательного выбора решения, то он по-прежнему остается прерогативой человека. Только человек, с его непревзойденным умением решать неформальные задачи, принимать так называемые «компромиссные решения» (не строго оптимальные, но приемлемые по ряду критериев) может взять на себя ответственность за окончательный выбор.

§ 9. Проблема выбора решения в условиях неопределенности

Раньше мы рассмотрели обратную задачу исследования операций в детерминированном случае, когда показатель эффективности W зависит только от двух групп факторов: заданных, заранее известных a и элементов решения х. Реальные задачи исследования операций чаще всего содержат помимо этих двух групп еще одну — неизвестные факторы, которые в совокупности мы обозначим одной буквой x. Итак, показатель эффективности W зависит отвсехтрех групп факторов: W = W(a, х, x).

Так как величина W зависит от неизвестных факторов x, то даже при заданных a и x она уже не может быть вычислена, остается неопределенной. Задача поиска оптимального решения тоже теряет определенность. Ведь не можем же мы максимизировать неизвестную величину W!

Переводя сказанное на математический язык, поставим перед собой следующую задачу.

При заданных условиях a, с учетом неизвестных факторов x, найти такое решение х Î X, которое, по возможности, обеспечивает максимальное значение показателя эффективности W.

Задача принятия решения в условиях неопределенности на каждом шагу встречается нам в жизни.

Пример. Планируется ассортимент товаров для распродажи на ярмарке. Желательно было бы максимизировать прибыль. Однако заранее неизвестно ни количество покупателей, которые придут на ярмарку, ни потребности каждого из них. Неопределенность налицо.

Другой пример: проектируется система сооружений, оберегающих район от паводков. Ни моменты их наступления, ни размеры заранее неизвестны. А проектировать все-таки нужно, и никакая неопределенность не избавит нас от этой обязанности.

Наконец, еще более сложная задача: разрабатывается план развития вооружения на несколько пет вперед. Неизвестны ни конкретный противник, ни вооружение, которым он будет располагать. А решение принимать надо!

Современная наука располагает рядом приемов, чтобы принимать решение в условиях неопределённости. Для этого надо знать, какова природа неизвестных факторов x, с какого вида неопределенностью мы в данной задаче сталкиваемся.

Рассмотрим наиболее благоприятный для исследования вид неопределенности. Это случай, когда неизвестные факторы x представляют собой случайные величины (или случайные функции), статистические характеристики которых (законы распределения, математические ожидания, дисперсии и т. п.) нам известны или в принципе могут быть получены. Такие задачи исследования операций мы будем называть стохастическими задачами, а присущую им неопределенность — стохастической неопределенностью.

Приведем пример стохастической задачи исследования операций. Пусть организуется или реорганизуется работа столовой с целью повысить ее пропускную способность. Нам в точности неизвестно, какое количество посетителей придет в нее за рабочий день, когда именно они будут появляться, какие блюда заказывать и сколько времени будет продолжаться обслуживание каждого из них. Однако характеристики этих случайных величин, если сейчас еще не находятся в нашем распоряжении, могут быть получены статистическим путем.

Другой пример: организуется система профилактического и аварийного ремонта технических устройств с целью уменьшить простои техники за счет неисправностей и ремонтов. Отказы техники, длительности ремонтов и профилактик носят случайный характер. Характеристики всех случайных факторов, входящих в задачу, могут быть получены, если собрать соответствующую статистику.

Показатель эффективности W, зависящий от этих факторов, тоже будет величиной случайной. Максимизировать случайную величину невозможно: при любом решении х она остается случайной, неконтролируемой. Как же быть?

Первый подход: заменить случайные факторы x их средними значениями (математическими ожиданиями). Тогда задача становится детерминированной и может быть решена обычными методами.

Этот прием в некоторых случаях оправданный. Весь вопрос в том, насколько случайны эти параметры: если они мало отклоняются от своих математических ожиданий, так поступать можно и нужно, т.к. в таких задачах случайностью можно пренебречь.

Тот же прием — пренебречь случайностью и заменить все входящие в задачу случайные величины их математическими ожиданиями — будет уже опрометчивым, если влияние случайности на интересующий нас исход операции существенно. Возьмем самый грубый пример: пусть мы ведем обстрел какой-то цели, стремясь во что бы то ни стало попасть в неё. Производится несколько выстрелов. Давайте заменим все случайные координаты точек попадания их математическим ожиданием— центром цели. Получится, что любой выстрел с гарантией попадет в цель, что заведомо неверно. Т. о. операции, в которые случайность входит по существу, свести к детерминированной задаче не удается.

Второй подход. Рассмотрим такую операцию 0, где факторы x «существенно случайны» и заметно влияют на показатель эффективности W, который тоже «существенно случаен».

Возникает мысль: надо взять в качестве показателя эффективности среднее значение (математическое ожидание) этой случайной величины и выбрать такое решение х, при котором этот усредненный поусловиям показатель обращается в максимум:

W = М [W (a, х, x)] ® mах

Такой подход называется «оптимизацией в среднем» и в большинстве случаев вполне оправдан.

Элемент неопределенности, конечно, сохраняется. Эффективность каждой отдельной операции, проводимой при конкретных значениях случайных факторов x может сильно отличаться от ожидаемой как в большую, так и в меньшую сторону. Оптимизируя операцию «в среднем», мы в конечном счете после многих ее повторений выиграем.

Надо, чтобы операция обладала свойством повторяемости, и «недостача» показателя эффективности в одном случае компенсировалась его «избытком» в другом.

Третий подход. Такое требование выполняется не всегда.

Чтобы убедиться в этом, рассмотрим пример. Организуется автоматизированная система управления (АСУ) для службы неотложной медицинской помощи большого города. Вызовы, возникающие в разных районах города в случайные моменты, поступают на центральный пункт управления, откуда они передаютсяна тот или другой пункт неотложной помощи с приданными ему машинами. Требуется разработать такое правило (алгоритм) диспетчерской работы АСУ, при котором служба в целом будет функционировать наиболее эффективно. Для этого, прежде всего, надо выбрать показатель эффективности W.

Разумеется, желательно, чтобы время Т ожидания врача было минимально. Но это время — величина случайная. Если применить «оптимизацию в среднем», то надо выбрать тот алгоритм, при котором среднее время ожидания минимально.

Беда в том, что времена ожидания врача отдельными больными не суммируются: слишком долгое ожидание одного из них не компенсируется почти мгновенным обслуживанием другого.

Например, в качестве показателя эффективности возьмём Т - время ожидания врача больными и устремим его к минимуму. Операция обладает свойством повторяемости, но «недостача» показателя эффективности в одном случае не компенсируется его «избытком» в другом. В этом случае можно дополнить показатель эффективности добавочным требованием, чтобы фактическое время Т ожидания врача было не больше какого-то предельного значения t_О. Поскольку Т — величина случайная, нельзя просто потребовать, чтобы выполнялось условие Т £ t_О; можно только потребовать, чтобы оно выполнялось с очень большой вероятностью, было практически достоверным. Назначим некоторое значение b, близкое к единице (например, 0,99 или 0,995), и потребуем, чтобы условие Т &pou

Дата добавления: 2014-01-07