Лекция 4. Развитие учения о строении атомов

Законы

Лекция 2. Основные стехиометрические

1. Закон Авогадро — Гей-Люссака. Молекулярные массы газов.

2. Расчет атомных масс. Составление формул химических соединений.

3. Вычисление эквиваленто простых и сложных веществ.

1. Закон Авогадро – Гей-Люссака. Молекулярные массы газов

В результате исследований газов и открытия газовых законов удалось определить состав молекул простых веществ, отыскать массы молекул и атомов и, в конце концов, определить химические формулы сложных веществ. Гей-Люссак, анализируя результаты экспериментов, пришел к выводу, что объемы реагирующих и образующихся в результате реакций газов относятся между собой как небольшие целые числа. Так, исходное соотношение объемов водорода и кислорода при образовании воды составляет 2: 1, а получается 2 объёма водяного пара. Имелись данные по реакции оксида серы (IV) С кислородом, оксида углерода (II)—угарного газа с кислородом и некоторым другим газовым реакциям. Гей-Люссаком был сделан вывод; у равных объемах различных газов при одинаковых давлениях и температуре содержится одинаковое число атомов. Если в 1 объеме одного газа (водорода) и в 1 объеме другого (хлора) содержалось одинаковое количество атомов (водорода и хлора), то должен был бы образоваться 1 объем газообразного продукта реакции (хлористого водорода), а образовывалось два объема. Следовательно, сделанный вывод противоречил этим экс­периментальным данным. Однако идея Гей-Люссака дала возмож­ность Амедео Авогадро высказать (1811) гипотезу, известную сей­час как закон Авогадро.

В равных объемах различных газов, при одинаковых условиях давления и температуры содержится одинаковое число мельчайших частиц (молекул).

Казалось бы разница по сравнению с формулировкой Гей-Люс­сака небольшая, но эта разница принципиальная. Образование 2 объемов хлористого водорода из 1 объема водорода и 1 объема хлора привело Авогадро к мысли, что каждая из мельчайших ча­стиц водорода и хлора состоит из 2 атомов. Аналогичные наблюде­ния были сделаны и в отношении реакций других простых газооб­разных веществ. Таким путем Авогадро пришел к заключению, что «мельчайшие частицы» большинства газообразных простых веществ при обычных условиях двухатомны, т. е. формулы простых газов Н₂, Сl₂, N₂ и т. п. Следствия из закона Авогадро настолько важны, что всю последующую химию стали называть «авогадрова химия». Этот закон, доказательство которого приведем несколько позже, позволил не только теоретически определить понятия «атома» и «молекулы», но предоставил практическую возможность для на­хождения молекулярных масс газообразных веществ, а затем и масс атомов входящих в них элементов.

Молекулярная масса вещества—средняя масса его молекулы, выраженная в углеродных единицах.

Атомная масса элемента—средняя масса природной смеси его атомов, выраженная в углеродных единицах.

Закон Авогадро позволил определять молекулярные массы га­зообразных веществ по их относительной плотности D_отн равной отношению масс т₁ и т₂ одинаковых объемов (например, 1 л) га­зов, взятых при одних и тех же давлении и температуре. Это отно­шение показывает, во сколько раз один газ тяжелее другого. Так как в равных объемах различных газов при равных условиях со­держится одинаковое число молекул N, то m₁=M₁N и m₂=M₂N и тогда D_отн равна отношению молекулярной массы одного газа М₁ к молекулярной массе М₂ другого:

D_отн = 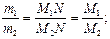М₁ = D_отн М₂

Обычно относительную плотность определяют либо по водороду D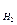либо по воздуху D_возд. Молекулярная масса двухатомной мо­лекулы водорода равна двум, точнее 2,016 у. е. Относительная плотность воздуха по водороду равна 14,5. Отсюда молекулярная масса воздуха равна 29 у. е. Экспериментально определяя относи­тельную плотность любого газообразного вещества по воздуху, легко вычислить молекулярную массу исследуемого газа:

М_х = 29D_возд или М_х = 2,016 D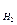

Для практического пользования введены понятия грамм-моле­кула (моль) и грамм-атом (моль атомов). Количество вещества № граммах, численно равное его молекулярной массе, называют мо­лем или грамм-молекулой.

Количество вещества в граммах, численно равное атомной массе элемента, называют моль атомом или грамм-атомом элемента. Так как равные объемы различных газов содержат при одинаковых условиях одно и то же число молекул, то моли различных газов будут занимать одинаковый объем. Если задаться конкретными условиями, то объем молекул любого газа становится не только одинаков, но и строго определен. В качестве условий для сравнения приняты нормальные условия (н. у.): давление 1,01 · 10⁵ Па (760 мм рт. ст.) и температура 0° С (273,18 К). При этих условиях моль любого газа занимает объем, равный 22,414 л.

Пример 1. При н.у. масса 1 л водорода равна m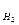= 0,09 г. Воздуха m_возд=1,29 г. У этих газов моли равны соответственно 2,016 и 29 г.

Решение. Объем моля газа равен:

V = 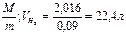и V_возд =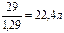

Молекулярную массу любого газа легко определить экспери­ментально, благодаря уравнению Менделеева—Клапейрона, вы­текающему из объединенного закона Бойля — Мариотта и Гей-Люс-сака:

PV / Т = const

Если Р и Т взять для нормальных условий, а V—объем 1 моль газа при н. у. (т. е. 22,414 л), то соотношение PV/T становится ве­личиной постоянной для любого газа. Эта величина для 1 моль обозначается R и получается уравнение Менделеева — Клапейрона для 1 моль РV = РТ или для n молей

PV = nRT

Константа R называется универсальной газовой постоянной. Фи­зический смысл R: работа расширения 1 моля любого газа при на­гревании на 1°. Численное ее значение определяется системой еди­ниц. Наиболее употребительные значения таковы: 0,082 лХ Хатм/(моль · К), 62 360 мл · мм рт.ст./ (моль · К), 8,3146 Дж/(моль Х

Х К).

Число молей n равно отношению экспериментально определяе­мого количества вещества к его молекулярной массе n=m/M. Зная массу любого объема газа при какой-то конкретной температуре и давлении, можно определить его молекулярную массу:

PV = (m/M) RT, M = mRT / PV

Пример 2. Опытным путем найдено, что 304 мл газа при 25°С, или 298 К, 745мм рт.ст. весят 0,78 г. Определить молекулярную массу газа.

Решение. Для удобства выбираем R = 62 360 мл · мм рт.ст. / (моль · К):

М = mRT / PV = 0,78 · 62 360 · 298 / 745 · 304 = 64 у. е.

Если этот газ простое вещество, следовательно, его молекула двухатомна, а атомная масса равна 32 у.е.

Моль любого вещества (и соответственно моль атомов) содер­жит одно и то же число частиц. Это одна из важнейших физико-хи­мических констант, названная в честь великого физика постоянной Авогадро N_А == 6,02252 • 10²³ моль-¹. Зная величину моля и na вхо­дящих и него частиц, можно найти массу одной частицы-молекулы. В рассмотренном выше примере 1 моль, т. е. все 6,02 ·10²³ молекул весят 64 г, а 1 молекула имеет массу

64 / (6,02 · 10²³) =1,06 · 10^-23 г.

Если молекула из двух атомов,то каждому из них соответствует масса, равная 0,53 · 10^-23 г.

2. Расчет атомных масс. Составление формул химических соединений

Закон Авогадро позволил определить массы молекул и атомов только для простых газообразных веществ. Однако на его основе Станислао Канниццаро создал метод расчета атомных масс эле­ментов, которые сами не являются газообразными, но образуют не­сколько летучих соединений. Идея метода проста: в молекуле не может быть менее одного атома. Следовательно, атомная масса элемента равна наименьшей его доле в различных соединениях.

По относительной плотности определяли молекулярные массы нескольких соединений одного и того же элемента. Затем путем анализа узнавали процентное содержание этого элемента в том или ином веществе. Отыскивали долю элемента — количество граммов его в 1 моле каждого вещества и минимальную величину из всех полученных принимали за атомную массу.

Пример 1. Требуется определить атомную массу углерода из следующих данных:

Соединение	Метан	Эфир	Винный спирт	Углекислый газ
М Содержание С,% Содержание С, г/моль	75,0	64,9	52,2	27,3

Из данных видно, что минимальное число частей от молекулярной массы ля углерода в соединениях 12. Этой доле кратны те, что приходятся на углерод других соединениях. Следовательно, атомная масса углерода равна 12. Точно таким же методом были найдены атомные массы фосфора, серы, хлора и других элементов, способных образовывать несколько газообразных или летучих со­чинений.

Пример 2. Вычислить атомную массу фосфора на основании следующих данных:

Вещество	Dвозд	М	Содержание Р, %
Хлорид фосфора Фосфористый ангидрид Фосфорный ангидрид Фосфористый водород	4,741 3,792 4,895 1,172	137,48 109,96 141,96 33,98	22,6 56,3 43,65

Решение. Вычислим количество массовых частей фосфора в соединениях, округляя получающиеся значения до целого числа.

22,6%	от	137,48	составляют		мас.	ч.
56,3%	,,	109,96	,,		,,	,,
43,65%	,,	141,96	,,		,,	,,
91%	,,	33,98	,,		,,	,,

Наименьшее число массовых частей будет соответствовать атомной массе фосфора А = 31.

Рассматриваемый метод пригоден только для элементов, образующих газообразные соединения. Им нельзя пользоваться для определения атомной массы элементов, у которых газообразные со­единения отсутствуют или их число невелико. Для них, очевидно, необходим принципиально иной метод определения атомной массы. Одна из возможностей определения для твердого вещества массы ⁸¹ атома элемента связана с увеличением энергии атома при нагревании твердого тела. Так как число атомов в моле атомов вещества всегда равно постоянной Авогадро, то для повышения температуры 1 моль атомов вещества на 1° требуется примерно одно и то же количество теплоты. Это впервые чисто эмпирическим путем было установлено в 1819 г. французскими исследователями Дюлон-гом и Пти. Произведение удельной теплоемкости С_уд твердого про­стого вещества на атомную массу А для большинства элементов равно 6,3. Иначе говоря, произведение

С_удА = 6,3

представляет количество теплоты, необходимой/для нагревания 1 моль атомов на 1°. Для большинства элементов в твердом состо­янии правило Дюлонга и Пти оказывается справедливым при ком­натной температуре. Поэтому зависимость использовалась для определения атомной массы элементов, находящихся при обыч­ных условиях в твердом состоянии.

Таким образом, цепочка рассуждений начинается от закона Аво-гадро. При помощи его получена формула, связывающая относи­тельную плотность и молекулярную массу. Зная молекулярную массу, по методу Канниццаро или Дюлонга — Пти находим атом­ную массу. И, наконец, используя атомные и молекулярные массы или эквиваленты, можно вывести формулы соединений.

Пример 3. Плотность химического вещества по водороду D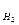 = 15. При анализе получено 80% С и 20% Н. Установить формулу соединения.

Решение. 1) атомная масса углерода 12, водорода 1. Допустим, что веще­ство содержит в моле х атомов углерода и у атомов водорода; 2) составляем пропорцию

12х: у = 80:20 или

х: у = 80 / 20: 20 / 1 = 6,7: 20 ≈ 1: 3.

Этому соотношению соответствует группа СН₃;

3) молекулярная масса составляет

М_Х = 2D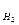= 30.

Следовательно, формула вещества С₂Н₆ – этан.

Пример 4. При анализе газообразного вещества определено что его плотность по водороду D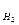= 15,95, а состав 87,5% азота и 12,5% водорода. Опре­делить простейшую и истинную формулы этого вещества.

Решение. Определим молекулярную массу вещества

M_x = 2,026D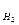= 32,15 у.е.

Соотношение азота и водорода в веществе

87,5 / 14: 12,5 / 1 = 6,25: 12,5 = 1: 2.

Простейшая формула NН₂.

Найдем истинную формулу:

а) количество азота в веществе

32,15 у. е. составляют 100% вещества

х у.е.,, 87,5%,, х = 28,13 у.е.

Количество атомов азота 28,13: 14 = 2,01 ≈ 2;

б) количество водорода в веществе

32,15 у.е. – 100%

у у.е. – 12,5% у = 4,02 у.е.

Число «томов водорода 4,02: 1,008 = 3,99 ≈ 4. Истинная формула N₂H₄.

Пример 5. Анализом определено содержание в веществе 87,44% Si и 12,56% Н, а плотность по воздуху D_возд = 1,108. Определить, что это за вещество и составить его формулу.

Решение: Молекулярная масса вещества

М_х = 29D_возд = 32,13 у. е.

Количество кремния в веществе

32,13 у. е. составляют 100%

х у.е.» 87,44% х = 28,09

Количество атомов кремния

28,09: 28,08 ≈ 1.

Количество водорода

32,13 у. е. составляют 100%

у у. е.» 12,56% у = 4,03

Количество атомов водорода

4,03: 1,008 ≈ 4.

Формула вещества SiH₄.

3. Вычисление эквиваленто простых и сложных веществ

Закон эквивалентов гласит: если массы двух элементов реагируют без остатка с одной и той же массой третьего элемента, то они могут без остат­ка реагировать и между собой.

Эквивалентом элемента называют количество ве­щества в молях, которое соединяется с молем атомов водорода или замещает то же количество атомов водорода в химических реакциях. Например, в молекула.х НС1 и NaCl 1 моль атомов водорода (1,0079г) эквивалентен 1 моль атомов натрия (22,9897 г).

Эквивалентной массой Э называют массу одного эквивалента вещества, выраженную в граммах (или килограммах) на моль. Например, эквивалентная масса кислорода составляет 8 г/моль.

Эквивалентная масса элемента равна молярной массе атомов элемента, деленной на его валентность в данном химическом соединении.

Пример 1. Вычислите эквивалентную массу серы (5§) всоединении, содержащем 5,92 % водорода и 94,08 % серы.

Решение. Составим пропорцию:

5,92 г водорода приходятся на 94,08 г серы

1 г/моль »»» Э г/моль» Э_S = 16 г/моль

Пример 2. Вычислите валентность углерода в соединения, содержащем 42,85% углерода и 57,15% кислорода.

Решение. Составим пропорцию:

42,85 г углерода приходятся на 57,15 г кислорода

Э г/моль »»» 8 г/моль» Э_С = 6 г/моль

Валентность углерода в этом соединении равна 2: моляр­ную массу (12 г/моль) делим на эквивалентную массу (6 г/моль).

Эквивалентная масса кислоты равна частному от деления ее молярной массы на основность кислоты.

Эквивалентная масса гидроксида равна частному от деления его молярной массы на валентность ме­талла.

Эквивалентная масса соли равна частному от де­ления ее молярной массы на произведение числа ионов металла и его валентности.

Пример 3. Определите эквивалентные массы следующих со­единений: Н₃РО₄, H₂SО₄, Са(ОН)₂, А1₂(SО₄)₃, Na₂CO₃,

Решение. Э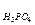= 98/3 = 32,7 г/моль; Э= 98/2 = 49 г/моль; Э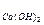= 74/2 = 37 г/моль; Э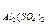342/6 = 57 г/моль; Э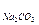= 106/2 = 53 г/моль.

Лекция 3. Важнейшие классы и номенлатура неорганических соединений

1. Оксиды.

2. Кислоты.

3. Основания. Амфотерные гидроксиды.

4. Соли.

Неорганические соединения делят на следующие классы: оксиды, гидроксиды (кислоты и основания), амфотерные гидроксиды, соли.

1. Оксиды

По международной номенклатуре соеди­нения элементов с кислородом называют оксидами; при обозначении этих соединений рядом с формулой или названием указывают в скобках степень окисле­ния элемента, например FeO—оксид железа (II), Fе₂О₃ – оксид железа (III). Оксиды разделяют на солеобразующие и несолеобраэующие. Солеобразующие, в свою очередь делят на кислотные, основные и амфотерные.

Кислотными (SO₂, CO₂ и др.) называют такие оксиды, которые образуют соли с основаниями или основными оксидами, например:

SO₂ + 2NaOH = Na₂SO₃ + Н₂О

Основными (CuO, FeO и др.) называют такие оксиды, которые образуют соли с кислотами или кислотными оксидами, например:

CuO + H₂SO₄ = CuSO₄ + Н₂О

Амфотерными называют оксиды металлов, образующие соли при взаимодействии как с кислотами (кислотными оксидами), так и с основаниями (основ­ными оксидами), например:

ZnO + 2НС1 = ZnCI₂ + Н₂О

ZnO + 2NaOH = Na₂ZnO₂ + Н₂О

Основные оксиды реагируют с кислотами и кислотными оксидами:

FeO + H₂SO₄ = FeSO₄ + Н₂О; MgO + SO₃ = MgSO₄

Оксиды щелочных и щелочноземельных метал­лов вступают во взаимодействие с водой:

СаО + Н₂O = Са(ОН)₂

Кислотные оксиды реагируют с гидроксидами, основными оксидами и (многие) с водой:

SO₂ + 2NaOH = Na₂SO₃ + H₂O; Р₂О₅ + ЗСаО = Cа₃(РO₄)₂;

SO₃ + H₂O = H₂SO₄

Способы получения оксидов:

взаимодействие веществ с кислородом

2Mg + О₂ = 2MgO: S + О₂ = SO₂

разложение гидроксидов, кислот

Сu(ОН₂) = СuО + Н₂О; 2Н₃ВО₃ = В₂О₃ + 3H₂O

разложение солей

СаСО₃ = СаО + СО₂

разложение оксидов

4СгО₃ = 2Сг₂О₃ + ЗО₂

взаимодействие кислот, обладающих окислительными свойствами, с металлами и неметаллами

С + 2H₂SO₄ (конц.) = СО₂ + 2SO₂ + 2Н₂О

2. Кислоты

Число атомов водорода, способных заме­щаться металлами с образованием солей, определяет основность кислоты. Различают кислоты однооснов­ные (например НС1, НNO₃), двухосновные (H₂SO₄, Н₂S), трехосновные (Н₃РO₄).

По химическому составу кислоты делят на бес­кислородные (HF, НС1 и др.) и кислородсодержа­щие (Н₂SО₄, HNO₃ и др.).

Большинство кислотных оксидов образует кис­лоты путем непосредственного присоединения воды. Кислотные оксиды называют ангидридами кислот. Молекулы некоторых ангидридов могут присоеди­нять разные количества молекул воды. При этом образуются метакислоты, содержащие наименьшее количество воды, и ортокислоты, содержащие наи­большее количество воды.

Например:

Р₂О₅ + H₂O = 2НРО₃ — метафосфорная кислота

Р₂О₅ + 2Н₂О = Н₄Р₂O₇ — пирофосфорная кислота

Р₂О₅ + 3Н₂О = 2Н₃РO₄ — ортофосфорная кислота

Название киcлот, в которых степень окисления центрального атома соответствует номеру группы в 1 таблице Д. И. Менделеева, образуется от русского (названия элемента с суффиксом «н» или «ов», на­пример: HNO₃ – азотная кислота, H₂WO₄ – воль­фрамовая кислота.

Если элемент имеет разные степени окисления и образует не одну кислоту, то в название кислоты с низшей степенью окисления элемента вводится суф­фикс «ист», например: Н₂SО₃ – сернистая кислота; HNO₂ – азотистая кислота.

Кислоты взаимодействуют с гидроксидами, основными оксидами, солями, металлами:

НС1 + NaOH = NaCI + Н₂О; H₂SO₄ + CuO = CuSO₄ + Н₂О

H₂SO₄ + 2NaCl = Na₂SO₄ + 2HC1; 2HC1 + Zn = ZnCI₂ + H₂↑

Некоторые кислоты разлагаются:

Н₂СО₃ = CO₂↑ + Н₂О

Определяют кислоты с помощью индикаторов: лакмуса, метилового оранжевого и др.

Способы получения кислот:

взаимодействие ангидридов, с водой

N₂O₅ + Н₂О = 2НNО₃

взаимодействие солей с кислотами

NaCI + H₂SO₄ = NaHSO₄ + НС1

окисление простых веществ

3P + 5HNO₃ + 2H₂O = 3H₃PO₄ + 5NO

соединение неметалла с водородом с последующим растворением полученного соединения в воде (по­лучение бескислородных кислот)

Н₂ + Сl₂ = НС1

3. Основания. Амфотерные гидроксиды.

В зависимости от числа гидроксильных групп основания бывают однокислотные (КОН, NaOH и др.) и многокислотные [Са(ОН)₂, Ва(ОН)₂ и др.]. Основания, растворимые в воде, называют щелочами. К ним относят основания, образованные щелочными и щелочноземельными металлами, и гидроксид аммония.

По международной номенклатуре основания на­зывают гидроксидами. Например, Fe(OH)₂ – гидроксид железа (II), Fе(ОН)₃ – гидроксид же­леза (III).

Амфотерные гидроксиды. Гидраты амфотерных оксидов, как и. сами оксиды, обладают амфотерными свойствами. С кислотами они взаимодействуют как основания

Zn(OH)₂ + H₂SO₄ = ZnSO₄ + 2H₂O

Основаниями – как кислоты:

H₂ZnO₂ + 2NaOH = Na₂ZnO₂ + 2H₂O

Гидроксиды реагируют с кислотными оксидами, с кислотами, с солями, некоторые при на­гревании разлагаются:

Са(ОН)₂ + СО₂ = СаСО₃↓ + H₂O; NaOH + НС1 = NaCI + Н₂О 2КОН + CuSO₄ == Cu(OH)₂↓ + K₂SO₄;

2Fе(ОН)₃ = Fе₂О₃ + ЗН₂О

Растворимые гидроксиды — щелочи определяют с помощью индикаторов: лакмуса, фенолфталеина, метилового оранжевого и др.

Гидроксиды получают взаимодействием:

щелочных и щелочноземельных металлов с водой

2Na + 2Н₂О = 2NaOH + H₂↑

оксидов щелочных и щелочноземельных металлов с водой

ВаО + Н₂О = Ва(ОН)₂

солей со щелочами (способ получения нераствори­мых гидроксидов)

FeSO₄ + 2NaOH = Na₂SO₄ + Fe(OH)₂↓

Щелочи также получают электролизом растворов солей калия, натрия.

4. Соли

Соли делят на средние (например, Na₂SO₄, Nа₂СО₃), кислые (NaHSO₄, NaHC0₃) и основные (NiOHNO₃,A1OHSO₄).

По международной номенклатуре название сред­них и кислых солей производят от названия кислот и металлов, их образовавших. Так: CuSO₄ – сульфат меди, К₂SO₃ – сульфит калия, NaHSO₃ – гидро­сульфит натрия, Nа₃РO₄ – фосфат натрия, NaHPO₄ – гидрофосфат натрия, NaH₂PO₄ – дигидрофосфат натрия.

Основные соли называют гидроксосоляма, напри­мер: NiOHNO₃ – нитрат гидроксоникеля, A1OHSO₄ – сульфат гидроксоалюминия.

Соли реагируют с солями, кислотами, щело­чами, водой, некоторые разлагаются при нагревании:

NaCI + AgNO₃ = NaNO₃ + AgCl↓;

СаСО₃ + 2HC1 = CaCI₂ + CO₂↑ + Н₂О

NiSO₄ + 2NaOH == Na₂SO₄ + Ni(OH)₂↓;

CuSO₄ + 5H₂O = CuSO₄ • 5Н₂О

MgCO₃ = MgO + CO₂↑

Средние соли получают взаимодействием:

металла с кислотой

Zn + H₂SO₄ (разб.) = ZnSO₄ + H₂↑;

Сu + 2Н₂SO₄(конц.) = CuSO₄ + SO₂↑ + 2Н₂О

основного оксида с кислотой

СаО + 2HC1 = CaCI₂ + Н₂О

гидроксида с кислотой

2NaOH + H₂SO₄ = Na₂SO₄ + 2Н₂О

соли с кислотой

СаСО₃ + 2НNО₃ = Сa(NО₃)₂ + CO₂↑ + Н₂О

основного оксида с кислотным

СаO + SiO₂ = CaSiO₃

гидроксида с кислотным оксидом

2КОН + N₂O₅ = 2КNО₃ + Н₂О

соли со щелочью

Fe(NO₃)₃ + 3NaOH == 3NaNO₃ + Fe(OH)₃↓

соли с солью

Ва(NО₃)₂ + Na₂SO₄ = BaSO₄↓ + 2NaNO₃

металла с солью

Fe + CuSO₄ = FeSO₄ + Cu↓

металла с неметаллом

Fe + S = FeS

металла со щелочью

Zn + 2NaOH = Na₂ZnO₂ + H₂↑

неметалла со щелочью

Сl₂ + 2КОН = КС1 + КС1O + Н₂0

неметалла с солью

Сl₂ + 2KI = 2КС1 + I₂

Средние соли можно получить также разложением кислородных солей при нагревании:

2КС1O₃ = 2КC1 + 3O₂↑

Способы получения кислых солей:

неполная нейтрализация кислоты или кислотного оксида гидроксидом

H₂SO₄ + NaOH = NaHSO₄ + Н₂О; CO₂ + NaOH == NaHCO₃

действие кислоты или кислотного оксида на нормальную соль той же кислоты:

Nа₂SO₄ + H₂SO₄ = 2NaHSO₄;

СаСО₂ + Н₂О = Са(НСО₃)₂

Основные соли чаще всего получают неполной нейтрализацией гидроксида кислотой:

Mg(OH)₂ + НС1 = MgOHCl + H₂O

Кислые соли можно перевести в средние прибавлением щелочи, а основные в средние—добавлением кислоты:

NaHCO₃ + NaOH = Na₂CO₃ + H₂O;

Fe(OH)₂Cl + 2НС1 = FeCI₃ + 2Н₂O

1. Основные положения современной теории о строении атомов.

2. Явление радиоактивности.

1. Основные положения современной теории о строении атомов

Доминирующей современной теорией электронов и других микрообъектов, обладающих очень малой массой, является квантовая механика. Оказалось, что законы движения мик­рообъектов принципиально отличаются от таковых для макрообъектов, к числу которых относятся все предметы, видимые в оптический микро­скоп и невооруженным глазом. Квантовая механика изучает движение микрообъектов в микрополях атомов, молекул и кристаллов. Из этого определения становятся очевидными роль и значение квантовой ме­ханики для современной химии. Не будет преувеличением сказать, что она синтезировала воедино наиболее актуальные проблемы физики и химии.

Главной особенностью квантовой механики является ее вероятност­ный статистический характер: она дает возможность на ходить вероятность того или иного значения некоторой физической величины. Объ­ясняется это волново-корпускулярным дуализмом микромира, т. е. микро­объекты обладают как корпускулярными, так и волновыми свойст­вами.

Не представляет труда обосновать объективность волново-корпускулярного дуализма для световых квантов – фотонов. Так, фотоэф­фект Столетова и эффект Комптона доказывают корпускулярную природу видимых и рентгеновских лучей, а их интерференция и дифракция — волновую природу света. Потому для фотонов легко по казать единство волны и корпускулы. Действительно, из формул следует Е = с²m = hν, откуда с учётом ν = с/λ получаем

с²m = h (с/λ)

или

λ = h / mc = h/р,

где λ — длина волны; р — количество движения или импульс фотона.

В 1924 г. французский ученый де Бройль высказал идею, что волново-корпускулярный дуализм присущ не только фотонам, но и всем микрообъектам. Поэтому, по де Бройлю, их движение связано с распространением волны, т. е. движение микрообъекта можно рассматривать как волновой процесс, при котором справедливо соотношение

Λ = h/ m₀υ

аналогичное для фотона. Формула связывает важнейшую характеристику вещественной формы существования матери (количество движения m₀υ) с характеристикой материального пол (длина волны λ) через постоянную Планка. Это и есть волново-корпускулярный дуализм.

Волновые свойства электронов, а вместе с ними идея де Бройля нашли экспериментальное подтверждение в опытах по рассеянию дифракции электронов, проведенных в 1927 г. в США, Великобритании и СССР. В Советском Союзе блестящие опыты по дифракции электронов были проведены в Ленинградском политехническом институте проф. Тартаковским П.С. Впоследствии опытным путем была обнаружена дифракция нейтронов, протонов, атоме гелия, молекул водорода других микрообъектов. В настоящее время волновые свойства материальных частиц широко применяются в методах исследования строения вещества — электронографии нейтронографии и др.

Однако идея де Бройля послужила только началом создания квантовой механики. Она рассматривала поведение микрообъекта, свободного от силового поля. В действительности же материальные частицы, например электроны, всегда находятся в поле действия определенных сил. С этой точки зрения электроны в атоме движутся в центрально- симметричном поле, для которого потенциальная энергия зависит только от расстояния до ядра. Законы движения в поле центральных сил образуют основу атомной механики: решение общей задачи о движении электронов в атоме опирается на результаты, относящиеся к движению одной частицы в поле центральных сил.

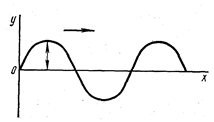
Рисунок 1. Распространение волны вдоль оси Х

На основе гипотезы де Бройля австрийский ученый Шрёдингер (1925—1926) интуитивно использовал волновое уравнение классиче­ской механики в качестве модели для описания поведения электрона в атоме. Из учения о колебаниях и волнах известно, что распростра­нение волны вдоль координатной оси х (рисунок) описывается дифференциальным уравнением в частных производных второго порядка

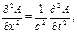
где А — амплитуда волны; с — скорость перемещения волны; t —время перемещения волны.

Но по Шрёдингеру, атомная сис­тема замкнутая, а потому поведение электрона, его движение подобно стоячей волне (рисунок). А математическое уравнение, описывающее стоячую волну, значительно проще, так как не содержит скорости и времени. Только атомная система в отличие от стоячей волны является трехмерной, а потому в уравнение для описания атомной стоячей волны Шрёдингер вводит все три аргумента: координаты х, у и z:

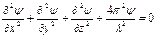
где ψ —трехмерный аналог величины А.

Рисунок 2. Стоячая волна

Теперь в выражение вместо λ подставим значение длины волны де Бройля, тогда получим

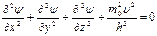
Полная энергия системы Е равна сумме потенциальной энергии U и кинетической (m₀υ²/2), т. е.

Е = U + (m₀υ²/2),

откуда υ² = 2 (Е - U) /m₀. Подставив это значение υ², по­лучим

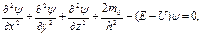
или, введя оператор Лапласа* 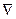² (набла в квадрате), запишем

где

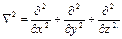
Выражение, а также есть волновое уравнение Шрёдингера для стационарного состояния, когда энергия системы не зависит от времени. В большинстве случаев задачи сводятся именно к нахождению стационарных состояний. Уравнения и не выводятся из более общих законов, а являются следствием эмпири­ческого выбора уравнения стоячей волны в качестве модели для опи­сания поведения электрона в атоме с учетом волны де Бройля. Право­мерность такого вывода уравнения Шрёдингера доказывается тем, что его решение приводит к значениям энергии Е, точно соответствующим опытным данным из атомных спектров.

Функция ψ в уравнении Шрёдингера называется волновой функ­цией. Физический смысл имеет величина ψ²dυ*, равная вероятности нахождения электрона в элементарном объеме dυ = dxdydz. Таким образом, квантовая механика дает лишь вероятность нахождения электрона в том или ином месте атомной системы. Поэтому такие по­нятия, как траектория частицы (например, электронная орбита), в квантовой механике не имеют смысла.

В соответствии с физическим смыслом ψ² сама волновая функция должна удовлетворять определенным условиям, которые называются стандартными условиями. Согласно последним волновая функция должна быть: 1) непрерывной, так как состояние квантовой системы в пространстве меняется непрерывно; 2) конечной, т. е. она не должна обращаться в бесконечность ни при каких значениях аргументов;

3) однозначной, ибо по смыслу ψ есть амплитуда вероятности, а потому для любой данной точки она может иметь только одно значение; 4) об­ращаться в нуль на бесконечности. Так, при рассмотрении поведения электрона в атоме ψ должна быть равной нулю на бесконечно большом расстоянии от ядра.

2. Явление радиоактивности

Явление радиоактивности было открыто в 1896 г. известным французским физиком Анри Беккерелем. Беккерель установил, что металлический уран, а также его минералы и соединения испускают невидимое излучение. Воздух по соседству е препаратами становится хорошим проводником электричества и раз­ряжает электроскоп. Излучение вызывало почернение фотографичес­кой пластинки, завернутой в черную бумагу или закрытой непрозрач­ными предметами. Излучательная способность не зависела от темпе­ратуры урансодержащего препарата, от его агрегатного состояния, а определялась только содержанием урана. Беккерель из этих наблю­дений сделал заключение, что способность к излучению является свой­ством атомов урана и не зависит от того, входит ли уран в состав сое­динения.

Вскоре было обнаружено, что излучательной способностью обла­дает и торий, а в 1898 г. супругами Марией и Пьером Кюри были от­крыты два новых химических элемента — радий и полоний. Излуча­тельная активность радия вместе с элементами, образующимися и» него, оказалась в миллион раз больше активности урана. Мария Кю­ри предложила термин радиоактивность для обозначения способности элементов к самопроизвольному излучению. В последующие годы были открыты еще некоторые радиоактивные элементы — актиний, эманации радия, тория и актиния (названные радоном, тороном, ак­тиноном) и многие другие. При этом каждое из выделенных радиоактив­ных простых тел рассматривалось как самостоятельный химический элемент. Количество подобных «элементов» превосходило число клеток в Периодической системе и некоторые из них обладали тож­дественными химическими свойствами с уже известными. Введение понятия изотопа уменьшило их число. Оказалось, что радон, торон, актинон являются разными изотопами одного и того же элемента. Поэтому они должны занимать одну клетку в Периодической системе. В дальнейшем изотопия стала важнейшим свойством для большинства химических элементов.

В 1913 г. Фаянс и Содди независимо друг от друга формулируют правила радиоактивного смещения:

1. При α-распаде возникает изотоп элемента, смещенного на две клетки от исходного к началу Периодической системы и имеющий на 4 единицы меньше массовое число.

2. β-Распад приводит к возникновению изотопа элемента, смещен­ного на одну клетку от исходного к концу Периодической системы с тем же массовым числом. Эти правила в еще большей степени способ­ствовали правильной расстановке радиоактивных элементов в Перио­дической системе и пониманию их химического поведения.

В том же 1913 г. Мозли дает в руки исследователей рентгеноспектральный метод определения положительного заряда ядра элемента, а следовательно, его места в Периодической системе. Это способство­вало поиску новых радиоактивных элементов и исправлению числен­ных значений порядковых номеров элементов. Была установлена пра­вильная последовательность превращений одних радиоактивных изо­топов в другие, открыты пропущенные звенья в цепи генетически связанных элементов — радиоактивных рядах.

В это время радиохимия как наука о химических и физико-химичес­ких свойствах радиоактивных элементов разрабатывает свои специ­фические методы исследования. В ее задачу входит широкий круг во­просов, связанных с проблемами разделения, очистки, концентрирования радиоактивных элементов.

Таким образом, открытие явления радиоактивности было важной вехой на пути познания окружающего мира. Изучение же радиоактив­ности дало неопровержимые доказательства сложности структуры атома. Оно стало основным фактом, опровергающим представления о неизменности атомов, и показало, что в определенных условиях одни атомы разрушаются, превращаясь в другие.

В 1919 г. Резерфорд впервые осуществил искусственное превращение элементов. Под действием α-частиц азот был превращен в кислород. В дальнейшем процессы взаимодействия ядер одних эле­ментов с ядрами других (или с элементарными частицами), при которых образовывались ядра новых элементов, стали называть ядерными реакциями. Чаще всего ядерные реакции представляют собой процес­сы взаимодействия ядер с частицами сравнительно небольшой массы (α-частицами, протонами, нейтронами, дейтеронами и т. д.). Обозна­чения, которые применяются при записи ядерных реакций, анало­гичны обозначениям, принятым при написании уравнений химичес­ких реакций. Символы ядер элементов, вступающих в реакцию, запи­сываются слева, а образующихся продуктов — справа. Над символом слева вверху указывается массовое число изотопа, а слева внизу его порядковый номер. Сумма верхних индексов с левой стороны равенства должна равняться их сумме справа. Это требование относится и к сумме нижних индексов. Реакция первого искусственно вызванно­го ядерного превращения, осуществленного Резерфордом, записы­вается так:

Нередко используется более короткая запись: символы легких частиц (бомбардирующих и образующихся), записывают в скобках между сим­волами исходного и конечного ядер. Тогда уравнение приведенной реакции запишется: .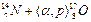

В ядерных процессах энергию относят к превращению одного ядра и выражают в электронвольтах. Энергетический эффект ядерных про­цессов неизмеримо больше тепловых эффектов обычных химических реакций. Так, например, реакция 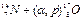имеет Δ Н = - 1,19МэВ, или —2,74 · 10¹⁰ кал/г-атом. Эта величина по крайней мере в 100 000 раз больше самых высоких значений тепловых эффектов хими­ческих реакций.

Ядерные реакции могут идти как с выделением, так и с поглощением энергии. Одним из наиболее известных примеров экзотермического ядерного превращения является реакция деления урана, сопровож­дающаяся выделением 180 МэВ. Для других ядерных процессов энер­гетические эффекты не столь значительны. Кроме того, надо иметь в виду, что ядерные реакции по сравнению с химическими представля­ют собой очень редкое событие. По-видимому, одной из причин этого является малый размер ядер, что делает маловероятными эффективные ядерные соударения. Установлено, что скорость радиоактивного рас­пада пропорциональна наличному числу ядер:

dN / dτ = - λN,

где dN/dτ — количество ядер, распадающихся в единицу времени, т. е. скорость распада; N — число имеющихся в данный момент радио­активных ядер. Коэффициент пропорциональности К называется по­стоянно и радиоактивного распада. Она равна доле ядер, распадающих­ся за единицу времени. Для каждого радиоактивного изотопа λ имеет определенное значение и не зависит от температуры, давления, элек­трического и магнитного полей, химического состояния радиоактив­ного изотопа, его концентрации.

Дата добавления: 2014-01-07