
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Характеристики САУ
|
|
|
|
1) Передаточная функция.
2) Частотные характеристики.
3) Переходная функция.
Преобразование Лапласа.
Наиболее общей характеристикой, определяющей динамические свойства САУ, являются ее дифференциальные уравнения. Чтобы исследовать динамику САУ, надо найти решение дифференциальных уравнений (или одного дифференциального уравнения высокого порядка) для этой системы. Однако нахождение решений дифференциальных уравнений, особенно высокого порядка, связаны со значительными трудностями. Например, для нахождения постоянных, входящих в решение и зависящих от начальных условий, надо решить систему алгебраических уравнений. В теории управления получил распространение способ нахождения решения дифференциальных уравнений с использованием операторных методов.
Операционный способ, называемый преобразованием Лапласа, упрощает нахождение решений дифференциальных уравнений. Принцип этого метода сводится к следующему: к дифференциальному уравнению, в которое входит как аргумент время  применяют прямое преобразование Лапласа. С помощью этого преобразования дифференциальное уравнение отображают на комплексную плоскость. В результате этого отображения дифференциальное уравнение преобразуется в алгебраическое, у которого аргументом является комплексная переменная
применяют прямое преобразование Лапласа. С помощью этого преобразования дифференциальное уравнение отображают на комплексную плоскость. В результате этого отображения дифференциальное уравнение преобразуется в алгебраическое, у которого аргументом является комплексная переменная  где
где 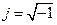 (вместо
(вместо 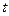 ).
).
Полученное алгебраическое уравнение можно разрешить относительно интересующей нас регулируемой величиныY(p). Но полученное решение будет функцией комплексного переменного. Для получения решения Y(t), как функции от времени,Y(p) нужно преобразовать с помощью обратного преобразования Лапласа.
Каждой функции X(t) вещественной переменной t, которая называется оригиналом, ставится в соответствие по некоторому закону другая функция X(p), называемая изображением. Соответствие выбирается таким образом, чтобы сложным операциям над оригиналом соответствовали бы простые операции над изображением. Например, чтобы операции дифференцирования оригинала соответствовала бы операция умножения, операции интегрирования – операция деления. Такое соответствие задается прямым преобразованием Лапласа
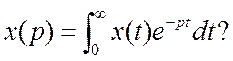
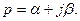
Соответствие оригинала и изображения записывают
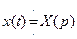
Для того, чтобы к функции X(t) можно было бы применить преобразование Лапласа, необходимо:
1) X(t) - была бы кусочно- непрерывной
2) 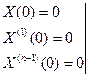


3) X(t) должна обладать ограниченной скоростью роста
 , где
, где 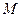 и
и  не зависят от
не зависят от 
Это означает, что X(t) должно расти медленнее, чем некоторая наперед заданная экспонента.
Имеются специальные таблицы для изображений элементарных функций.
Например:
1


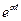

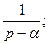

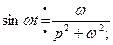

Напомним еще раз, что изображение является функцией комплексной переменной 
Некоторые свойства преобразований Лапласа
1. Свойство линейности
Если 
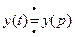 и α и β произвольные числа, то
и α и β произвольные числа, то


2. Теорема о дифференцировании оригинала
Если  , то
, то
 , или в общем виде:
, или в общем виде:
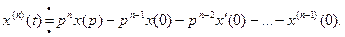
При отображении на комплексную плоскость дифференциального уравнения при нулевых начальных условиях

Дифференцирование оригинала при нулевых начальных условиях заменяется умножением изображения на  в соответствующей степени.
в соответствующей степени.
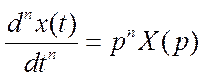 .
.
3. Интегрирование оригинала
Если  , то
, то

Интегрирование оригинала соответствует делению на 
4.Теорема запаздывания
Если  и
и  , то
, то
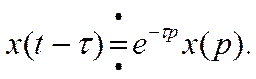
5. Теорема о свертке
Свертке во множестве оригиналов соответствует обычное произведение функций во множестве изображений.

6. Теорема разложения
Если 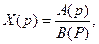 где
где 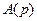 и
и  - многочлены и порядок
- многочлены и порядок  больше порядка
больше порядка 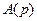 , то оригинал
, то оригинал
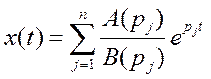 ,
,
здесь  - корни уравнения
- корни уравнения 
7. В общем случае оригинал находится по изображению


Интегрирование производится вдоль прямой, параллельной мнимой оси и отстоящей от нее на 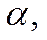
 произвольная константа, удовлетворяющая условию
произвольная константа, удовлетворяющая условию 
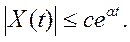
Пример решения дифференциального уравнения с помощью преобразования Лапласа.
Найти решение уравнения

Начальные условия (не нулевые)
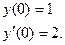
Используя свойство линейности и теорему о дифференцировании оригинала, получаем
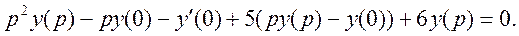
Отсюда

Отсюда

Для нахождения решения дифференциального уравнения применим теорему разложения.
У нас 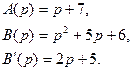
Корни уравнения 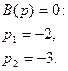
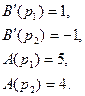
Тогда

ПЕРЕДАТОЧНЫЕ ФУНКЦИИ.
Задачи синтеза и анализа, а также исследование динамики САУ удобно решать, используя передаточные функции.
Пусть поведение системы описывается дифференциальным уравнением
 (1)
(1)
x(t) – входная величина
y(t) – выходная величина
Отобразим это уравнение на комплексную плоскость, используя прямое преобразование Лапласа при нулевых начальных условиях, свойство линейности и теорему о дифференцировании оригинала.
Пусть  ,
, 
Получим
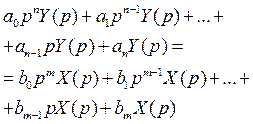 (2)
(2)
Таким образом отобразив дифференциальное уравнение с помощью преобразования Лапласа на комплексную плоскость, мы получим алгебраическое уравнение

Передаточной функцией называется отношение изображения Лапласа выходной величины к изображению Лапласа входной величины при нулевых начальных условиях.

 всегда правильная дробь. Знаменатель передаточной функции ха-
всегда правильная дробь. Знаменатель передаточной функции ха-
рактеризует инерционные свойства САУ.
 условие физической осуществимости реальной САУ.
условие физической осуществимости реальной САУ.
Знаменатель передаточной функции, приравненный к нулю, называется характеристическим уравнением


По передаточной функции можно найти установившееся значение выходной величины при подаче на вход единичного ступенчатого воздействия.
Используя предельные соотношения преобразования Лапласа, можно записать
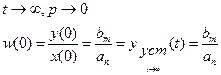
 - астатические системы,
- астатические системы,
 - статические системы.
- статические системы.
Например,



 - астатическая система
- астатическая система
Можно решать обратную задачу
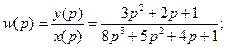
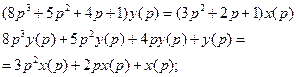
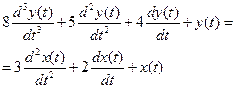
Свойства передаточных функций
Пусть  - корни характеристического уравнения,
- корни характеристического уравнения,
 - корни полинома числителя.
- корни полинома числителя.
Тогда
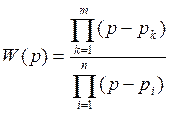
Если 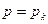 , то
, то 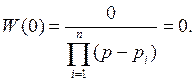
Поэтому корни полинома числителя называются нулями передаточной функции.
Если  , то
, то 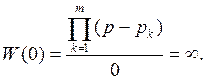
Поэтому корни полинома знаменателя, т.е. характеристического уравнения, называются полюсами передаточной функции.
Передаточная функция элемента с несколькими входами

Пусть на входе динамического элемента подаются сигналы 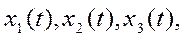
 а на выходе
а на выходе 
Пусть динамика элемента описывается дифференциальным уравнением

Тогда

Отсюда


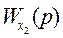

Коэффициенты перед  называются передаточными функциями по отношению к соответствующим входам.
называются передаточными функциями по отношению к соответствующим входам.
Изображение выходного сигнала элемента с несколькими входами равно сумме произведений изображений входов на передаточные функции по отношению к ним.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1033; Нарушение авторских прав?; Мы поможем в написании вашей работы!