Система плоских прямоугольных координат Гаусса-Крюгера

При создании планов местности большое значение имеет выбор направления осей системы прямоугольных координат и точки начала отсчета координат. В принципе, для каждого небольшого участка можно выбрать свою собственную систему координат и составить план в такой «местной» системе. Однако при этом нельзя будет сравнить или объединить планы даже двух соседних участков, если каждый из них будет составлен в своей условной системе координат.

Поэтому, как правило, необходима единая система координат, которая позволяет объединить материалы, выполненных на поверхности Земли съемок. Введение единой системы координат для всего земного шара или государства имеет большое значение. В этом случае обеспечивается возможность общего картографирования страны, когда каждый план становится частью общей карты государства.

Поверхность эллипсоида не может быть развернута на плоскость без искажений. В связи с этим проектирование точек поверхности эллипсоида на плоскость производится по определенным математическим законам. В общем виде вид закона проектирования можно представить следующими зависимостями

. (7.1)

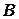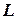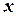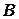Эти формулы означают, что каждой точке на эллипсоиде с геодезическими координатами и соответствуют плоские прямоугольные координаты и , как функции координат и 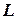точек поверхности эллипсоида на плоскости. Выбирая под разными условиями вид функци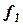й и 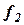, получают разные проекции.

В геодезической практике удобнее всего использовать равноугольные (конформные) проекции. В таких проекциях сохраняется равенство углов при переходе с поверхности эллипсоида на плоскость.

Теория конформного изображения одной поверхности на другую и, в частности, изображения поверхности земного эллипсоида на плоскости была разработана немецким ученым К.Ф. Гауссом в 1825-1830 годах, но практическое использование она получила после выведения Л. Крюгером в 1912 году рабочих формул, удобных для вычислений в этой проекции. Поэтому указанную проекцию называют проекцией Гаусса-Крюгера. В СССР система координат Гаусса-Крюгера была принята в 1928 году постановлением III Геодезического совещания в качестве общегосударственной системы координат для топографо-геодезических работ. Она и в настоящее время является основной системой координат при обработке геодезических измерений в Украине.

При использовании проекции Гаусса-Крюгера поверхность эллипсоида разделяется меридианными плоскостями на зоны (рис. 7.1).

 

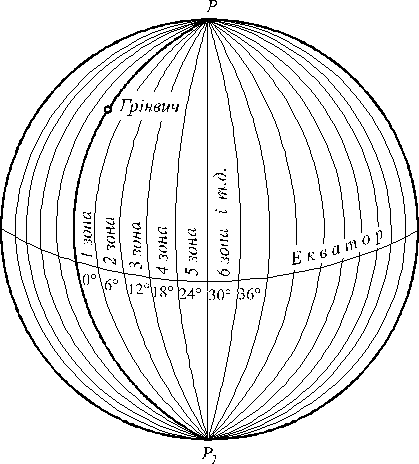
Рисунок 7.1 – Деление поверхности эллипсоида на координатные зоны

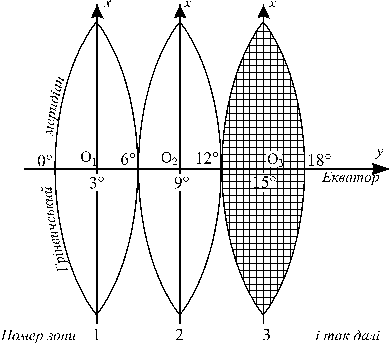
В Украине ширина зон по долготе установлена в 6º, а в районах, в которых выполняются топографические съемки в крупных масштабах – в 3º. Средний меридиан зоны называется осевым. Каждая их этих зон на плоскости образует самостоятельную систему координат (рис. 7.2). В результате такого проектирования получают изображение поверхности земного шара (эллипсоида) в виде зон, которые прилегают друг к другу на экваторе (рис. 7.3). Осевой меридиан каждой зоны изображается на плоскости прямой линией и принимается за ось абсцисс 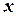. Экватор также изображается прямой линией, перпендикулярной к осевому меридиану. Он принимается за ось .

 

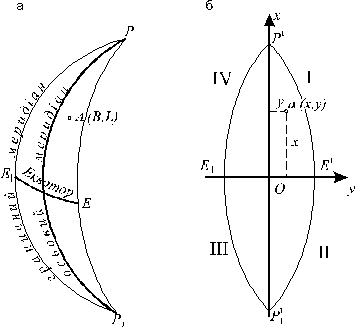
Рисунок 7.2 – Координатная зона: а) на эллипсоиде; б) на плоскости

 

Рисунок 7.3 – Системы координат для отдельных зон

Эти оси образуют прямоугольную систему координат зоны. Таким образом, в геодезии, в отличие от математики, используется левая система координат, в которой отсчет четвертей ведется по часовой стрелке (рис. 7.2, б). Это позволяет использовать в геодезических вычислениях формулы тригонометрии без каких-либо изменений. Абсциссы в системе координат Гаусса-Крюгера отсчитываются от экватора на север и юг; на север от экватора абсциссы положительные, а на юг – отрицательные. Ординаты на восток от осевого меридиана имеют знак плюс, на запад – минус.

Таким образом, в северном полушарии на всей территории Украины абсциссы всегда положительные, а ординаты могут быть как положительными (точка 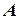на рис. 7.4, а), так и отрицательными. (точка 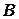на рис. 7.4, а)

 

Рисунок 7.4 – Условные ординаты в шестиградусных зонах

Чтобы избежать отрицательных значений ординат, начало координат переносят на 500 км к западу от осевого меридиана, как показано на рис. 7.4,б. Полученные таким образом ординаты называют условными и обозначают .

Условные ординаты вычисляют по формуле

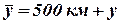(7.2)

Если, например, , а , то , . При обратном переходе от приведенных условных ординат необходимо отнять 500 км.

Для удобства определения прямоугольных координат при решении практических задач на планах и картах нанесена координатная сетка (рис. 7.3 и 7.4), которая представляет собой систему взаимно перпендикулярных линий, проведенных через определенные расстояния параллельно осевому меридиану зоны (ось ) и экватора (ось ).

Если заданы плоские прямоугольные координаты 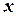и некоторой точки 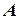, то этого недостаточно для однозначного определения положения точки, потому что точка с такими координатами есть в каждой зоне. Поэтому, необходимо указывать еще и номер зоны, в которой размещена точка. Он указывается перед каждой ординатой. Например, точка 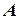находится в 7-й зоне, тогда ее полная условная ордината .

В Украине, как и в бывшем СССР и теперь в России, принято такое правило разбивки территории на зоны..

Дата добавления: 2014-01-07