Тема 15

Обратная геодезическая задача

Прямая геодезическая задача

Главные геодезические задачи

Тема 14.

Вычислительная обработка результатов измерений на местности, проводимая при составлении планов, решение ряда землеустроительных задач, подготовка данных для выноса проектов в натуру непосредственно связаны с прямой и обратной геодезическими задачами на координаты.

Сущность прямой геодезической задачи (рис.): по известным координатам точк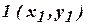и линии 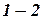, дирекционному углу этой линии 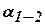и ее горизонтальному проложению 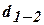требуется определить координаты точки .

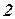Проведя через точк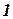и и 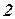линии, параллельные координатным осям, получим прямоугольный треугольник 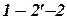, в котором известны гипотенуза 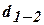и острый угол 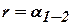. Катеты этого треугольника есть приращения координат 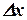и 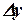, которые могут быть получены по формулам:

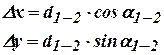(13.18)

Контроль:

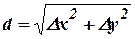. (13.19)

Следует помнить, что в общем случае знаки приращений координат зависят от четверти, определяемой дирекционным углом заданного направления (см. табл.13.1).

Тогда координаты искомой точки 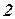определяются по формулам

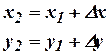(13.20)

или

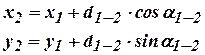(13.21)

Приращения координат и координаты искомой точки вычисляются с точностью, соответствующей точности измерения горизонтальной длины линии.

Сущность обратной геодезической задачи: по известным координатам точек 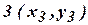и 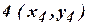требуется определить горизонтальное проложение стороны 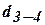и дирекционный угол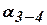

Согласно рис. и формулам (18) можно записать

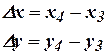(13.22)

По найденным значениям приращений координат 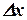и 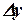, решая прямоугольный треугольник, вычисляют табличный угол

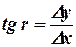, (13.23)

откуда

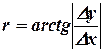(13.24)

По знакам приращений координат 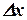и 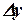определяют, в какой четверти находится данное направление. Затем, руководствуясь соотношением между табличным и дирекционным углами (см. табл. 13.1), находят дирекционный угол направления. Например, в рассматриваемом случае знаки приращений координат показывают, что направление 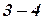находится в 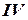четверти, тогда

.

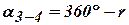Зная дирекционный угол направления и приращения координат, определяют горизонтальное проложение стороны.

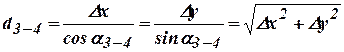(13.25)

По формуле (13.25) значение горизонтального проложения стороны определяется трижды: сходимость результатов служит надежным контролем решения задачи. Наибольшее внимание при решении обратной задачи следует уделять вычислению приращений координат 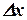и .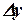

Дата добавления: 2014-01-07