Фазовые равновесия

МАССООБМЕН.

Конспекты лекции

Массообменные процессы и аппараты

Н.Х. Зиннатуллин

Казань, 2012

Основная задача химико-технологического процесса состоит в направленном изменении макроскопических свойств участвующих в процессе веществ: состава, агрегатного состояния, давления P и температуры Т. При этом происходит перенос субстанций: массы, энергии, импульса. Предельное состояние системы – подвижное равновесие, при котором не происходит изменений макроскопических свойств веществ. Равновесным называют такое состояние системы, при котором перенос субстанций отсутствует.

В изолированной системе условия равновесия определяется только внутренними условиями и записываются так:

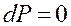, , (1.1)

Здесь, 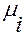– химический потенциал 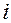-того компонента.

Условия (1.1) называют условиями механического, термического и химического равновесия.

Все самопроизвольные процессы сопровождаются увеличением энтропии системы. В состоянии равновесия энтропия достигает максимального значения:

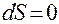(1.2)

Таким образом, условия равновесия системы определяются уравнениями (1.1) и (1.2).

Для открытой системы равновесное состояние может быть устойчивым лишь при её равновесии с окружающей средой. Движущая сила процессов переноса возникает вследствие отклонения от равновесия в самой системе или в окружающей среде. Все технологические схемы является открытыми системами.

Химический потенциал 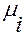зависит не только от концентрации данного компонента, но и от вида и концентрации других компонентов системы.

Химический потенциал компонента непосредственно изменить невозможно. Для его расчета используют соотношения между термодинамическими функциями, которые, в свою очередь, зависят от состава смеси. Поэтому в инженерных расчетах для определения движущей силы процесса используют разность концентраций.

Возможное существование данной фазы в равновесии с другими определяется по закону равновесия фаз Гиббса:

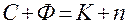(1.3)

Здесь С – число степеней свободы (Р,Т и концентрация) – минимальное число параметров, которые можно изменять независимо друг от друга, не нарушая равновесие данной системы; 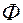– число фаз системы; – число независимых компонентов системы; – число внешних факторов, влияющих на положение равновесия в данной системе.

Для процессов переноса массы =2 (давление и температура).Правило фаз Гиббса определяет возможность существования фаз, но не указывает на количественных зависимостей переноса вещества между фазами.

Обычно зависимости между параметрами строят в плоских координатах. Такие диаграммы называются фазовыми.

Для бинарной смеси строят следующие фазовые диаграммы: –при Т=const, Т–при =const, y(x)–при T=const, y-x при =const. Здесь

- концентрация, y и x – концентрация вещества в фазах.

Рис.1.1. Схема массообменного процесса.

Рассмотрим пример поглощения аммиака чистой водой из аммиачно-воздушной смеси: у - концентрация аммиака в воздухе, х - концентрация аммиака в воде. Аммиак - распределяемый компонент. С началом растворения аммиака в воде начнётся переход части его молекул в обратном направлении со скоростью, пропорциональной концентрации аммиака в воде. С течением времени скорость переноса аммиака в воду будет снижаться, а скорость обратного переноса возрастать. Такой двусторонний перенос будет продолжаться до установления динамического равновесия – когда переходы в обоих направлениях будут равны.

При равновесии достигается определённая зависимость между равновесными концентрациями распределяемого вещества в фазах при Т и= const:

, (1.4)

где у* - равновесная концентрация аммиака в воздухе, при концентрации аммиака в воде х.

Графическое изображение зависимости (1.4) и есть линия равновесия. Эту зависимость представим в виде:

у* = mx (1.5),

где m – коэффициент распределения.

Для двухкомпонентной двухфазной системы коэффициент распределения будет зависеть от двух переменных m=f(T,x)=f(,x)=f(,T).

Следовательно, необходимо иметь набор экспериментальных данных по равновесию по всей области изменения двух параметров. При увеличении числа компонентов в системе ситуация ещё более усложняется. При отсутствии таких экспериментальных данных для определения коэффициента распределения можно использовать аналитические зависимости. Такие зависимости рассмотрены у А.И. Разинова и В.Б. Когана. Конкретный вид равновесия (1.5) различен для разных процессов массообмена. Например, для абсорбции равновесие описывается законом Генри, для ректификации – законом Рауля и т.д. Зная линию равновесия и рабочую линию для конкретного процесса можно определить направление и движущую силу массообмена в любой точке аппарата.

Дата добавления: 2014-01-07