Формула Хартли

Энтропия

На самом деле, по формуле Шеннона мы находим значение энтропии.

Энтропия – это мера неопределённости ситуации. Чем большее количество разных событий мы ожидаем, тем энтропия выше (то есть, тем больше неопределённость, какое же из ожидаемых событий действительно произойдёт).

Количество получаемой нами информации равно величине снимаемой этой информацией неопределённости.

То есть, количество информации = размер устранённой энтропии

Ввиду этого равенства мы можем утверждать, что по формуле Шеннона мы находим как энтропию, так и количество информации, необходимое для устранения этой энтропии.

Ожидаемые события могут быть равновероятны или не равновероятны. В нашей задаче с шарами события не равновероятны: белых шаров больше и вероятность того, что будет вынут белый шар, выше.

Если в формуле Шеннона все pi будет равны между собой (если все события равновероятны), тогда формула (1) превратится в формулу Хартли:

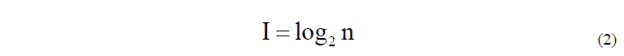
где I – количество информации (в битах) или энтропия до наступления события;

n – общее количество ожидаемых равновероятных событий.

Задача. Уровняем шансы: перекрасим 5 белых шаров в красный и ещё 5 белых шаров в синий цвет. Тогда в мешке будет 20 белых, 20 красных и 20 синих шаров. Выясним теперь, сколько информации мы получим, если узнаем, какого цвета наугад вынутый шар.

Решение. Можно было бы вести расчёт по формуле (1), но поскольку в данном случае события равновероятны, воспользуемся формулой (2). В нашем случае возможны три исхода: 1) либо достали белый; 2) либо достали красный; 3) либо достали синий. То есть, n = 3.

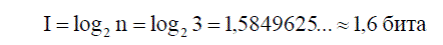
Видим, что величина исходной энтропии увеличилась (соответственно увеличилось количество информации, получаемой при устранении исходной энтропии).

Действительно, когда у нас белых шаров было больше, мы заранее могли предполагать, что будет вынут белый шар. А теперь мы находимся в большей неопределённости: ничего заранее предполагать не можем.

Вывод: Энтропия выше в том случае, если ожидаемые события равновероятны. Или иными словами: при наступлении события мы получаем информации больше в том случае, если ожидаемые события равновероятны.

Дата добавления: 2014-01-07