Плоская система сходящихся сил и условие ее равновесия

Тема 4. Системы сил и условия их равновесия

Лекция №2 Плоская система сходящихся сил.

Цель: Изучить плоскую систему сходящихся сил и ее равновесие.

Воспитательная цель: Показать применение математических методов при решении технических задач.

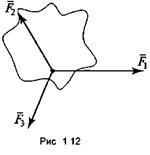
Плоской системой сходящихся сил называется система сил, линии дей­ствия которых лежат в одной плоскости и пересека­ются в одной точке (рис. 1.12).

Чтобы выяснить, будет ли данное тело находить­ся в равновесии под действием плоской системы схо­дящихся сил, необходимо найти ее равнодейству­ющую силу.

Если равнодействующая равна нулю, си­стема находится в равновесии, если не равна нулю — не находится в равновесии. Существует два способа определения равнодей­ствующей силы плоской системы сходящихся сил: геометрический и аналитический.

Геометрический способ определения равнодейству­ющей — построение силового многоугольника: в про­извольно выбранную точку переносится объект рав­новесия, в эту точку помещается начало первого вектора, перенесенного параллельно самому себе; к концу первого вектора переносится начало вто­рого вектора, к концу второго — начало третьего и т.д.

Если построенный силовой многоугольник окажется незамкнутым, зна­чит, данная система сил не находится в равновесии. В этом случае вектор равнодействующей силы соединит начало первого вектора с концом послед­него (рис. 1.13, а).

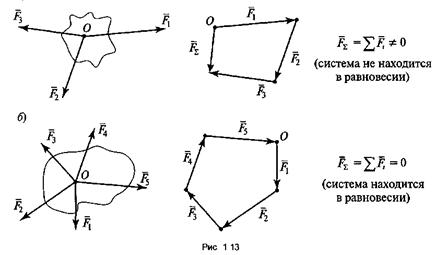Геометрическое условие равновесия плоской системы сходящихся сил за­ключается в замкнутости силового многоугольника, т.е. при построе­нии силового многоугольника конец последнего вектора совпадает с нача­лом первого (рис. 1.13,6).

Аналитический способ определения равнодействующей: все силы проекти­руются на две взаимно перпендикулярные оси координат, а затем находится алгебраическая сумма проекций всех сил на ось х и ось у. Если алгебраичес­кая сумма проекций всех сил равна нулю, данная система сил находится в равновесии. Аналитическое условие равновесия плоской системы сходящихся сил:

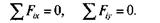
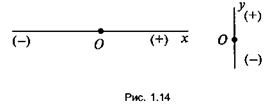
Осью координат называется произ­вольно выбранный направленный от­резок прямой (рис. 1.14).

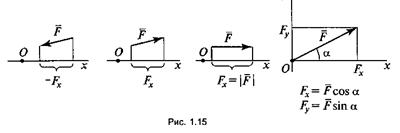
Проекция силы на ось координат — отрезок оси, отсекаемый перпендику­лярами, опущенными из начала и кон­ца вектора (рис. 1.15).

Дата добавления: 2014-01-07