Прямозубая передача

Расчет параметров зубчатого колеса. При вращении зубчатых колес име­ют место окружности, которые катятся друг по другу без скольжения с угло­выми скоростями, обратно пропорциональными их диаметрам (рис. 3.5). Та­кие окружности называются начальными или делительными. Физически они не существуют, понятие о них введено для построения теории зацепления. В основе расчета зубчатых колес лежит модуль.

Модулем называется отношение диаметра делительной окружности d к числу зубьев s

Модуль строго стандартизиро­ван. Для работы зубчатой пары мо­дуль у обоих колес должен быть один и тот же. Модуль характеризу­ет величину зуба. В зубчатой паре меньшее из колес называется шес­терней, большее — колесом. Дели­тельная окружность делит зуб на две части: верхнюю — головку и нижнюю — ножку. Для нормального зуба (рис. 3.6) высота головки и высота ножки равны соответственно

Полная высота зуба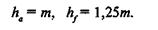

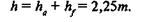
Радиальный зазор в зацеплении

Диаметр начальной окружности

d = mz.

Окружность, проходящая через вершину зубьев, называется окружностью выступов, а проходящая через основание зубьев, — окружностью впадин.

Диаметр окружности выступов и диаметр окружности впадин равны со­ответственно

d_a — d + 2т = m(z + 2),

d_f = d—2h= d— 2,5m = m(z — 2,5).

. Межосевое расстояние

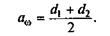
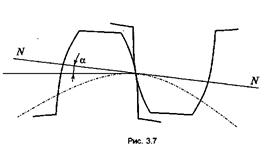
Линия и угол зацепления. Точка соприкосновения зубьев от начала зацеп­ления до выхода перемещается по прямой NN (рис. 3.7), которая называется линией зацепления. Угол, под которым линия зацепления наклонена к общей касательной на­чальных окружностей, называется углом зацепления. Стандартный угол зацепления α = 20°.

Коррегирование и подрезание. Коррегированием называется изменение высо­ты или профиля зуба (рис. 3.8). Корре­гирование бывает высотное и угловое. Коррегирование делается в целях уве­личения прочности, создания компакт­ности, корректирования межосевого рас­стояния.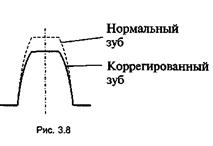

Если α = 20°, зуб будет с угловым коррегированием. При α > 20° зуб тол­ще, при α < 20° зуб тоньше.Для того чтобы не было заклинивания при большом передаточном отно­шении, иногда делается подрезание зубьев.

Силы взаимодействия в зубчатой паре. Сила взаимодействия между зубья­ми F_n всегда направлена по линии зацепления (рис. 3.10). Перенесем эту силу на ось симметрии зуба в точку О и разложим на две составляющие F_t и F_r. Таким образом, сила взаимодействия между зубьями дает две составля­ющие — окружную F_t и радиальную F_r силы:

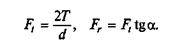
Угол α = 20°, tgα = 0,364.

Передаточное число. Существует понятие передаточного числа. Обозна­чается и. Передаточное число — это отношение параметров колес:

КПД прямозубой передачи - 0,96.

Сборник лекций для студентов групп НПО

Дата добавления: 2014-01-07