Средняя арифметическая

Понятие средних.

Статистика изучает совокупности по варьирующим признакам, среди которых важное значение занимают признаки, у которых вариация проявляется в изменении количественных значений.

Средней величиной в статистике называетсяобобщающая характеристика совокупности однотипных явлений по какому-либо варьирующему признаку, которая показывает уровень признака, отнесенная к единице совокупности. Средняя величина отражает общие, типичные черты, свойства явлений. Средняя величина может давать обобщенную характеристику лишь в пределах однородных явлений в пределах определенного типа явлений, следовательно, метод средних величин должен применяться в неразрывной связи с методом группировок.

Способы расчета средней могут быть разными, и в связи с этим в статистике различают несколько видов средней величины, основными из которых являются: Средняя арифметическая; Средняя гармоническая; Средняя геометрическая; Средняя квадратическая; Средняя кубическая и Структурные средние

Рассмотрим отличительные особенности отдельных видов средней величины.

Средняя арифметическая – это наиболее распространенная форма средней, применяемой в экономических расчетах.

Обозначим каждую варианту совокупности через х₁, х₂, х₃, и так далее х_п,, где п – число вариант, а среднюю величину – 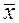, то:

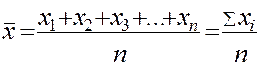
Средняя арифметическая в этой форме называется средней арифметической простой, так как она получена путем простого суммирования количественных значений варьирующего признака и делением этой суммы на число вариант.

Если данные представлены в виде дискретных или интервальных рядов распределения, в которых одинаковые значения признака (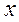) объединены в группы, имеющие различное число единиц (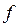), называемое частотой (весом), применяется средняя арифметическая взвешенная:

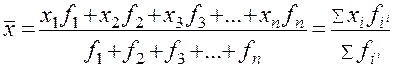
При расчете показателей вариации по интервальным рядам распределения необходимо сначала определить середины интервалов, а затем вести дальнейшие расчеты, рассматривая ряд середин интервалов как дискретный ряд распределения. Середина интервала находится следующим образом:

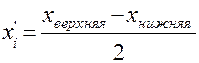
Основные правила расчета средней:

1. при расчете средней арифметической взвешанной по данным вариационного ряда частотами (весами) всегда являются числа, показывающие, сколько раз повторяется каждое значение осредняемого признака, положенного в основу группировки элементов совокупности. Сумма этих частот равна объему численности данной совокупности.

Осредняемые признаки	Веса средней
Месячная заработная плата рабочего, руб.	Численность рабочих, получающих заработную плату
Выработка рабочего за месяц, штук	Численность рабочих, занятых на данной работе
Выработка в час, штук	Количество отработанных часов
Себестоимость единиц продукции, руб.	Количество произведенной продукции
Энергетическая мощность предприятий	Количество предприятий

2. частоты вариационного ряда не могут служить весами для определения средней, если единица измерения признака, положенного в основу группировки не совпадают с единицей измерения элементов совокупности.

3. средняя рассчитанная по данным интервального ряда является приближенной. Чем уже интервал, тем меньше ошибка расчета.

4. веса средней может быть выражена в виде произведения: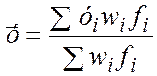

Дата добавления: 2014-01-07