
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Этап. Измерительный эксперимент
|
|
|
|
При проведении эксперимента в нормальных условиях получен результат:
Измерение массы изделия в воздухе:
mвозд = 9.9 кг
Измерение массы изделия в воде:
mвода = 9,15 кг
4 этап. Обработка экспериментальных данных.
Снижение массы изделия в воде составило
D mх = 0,75 кг.
По расчету (при mAu = 8 кг и mAg = 2 кг) снижение массы изделия должно быть:
D mр = 0,6 кг.
Значит в изделии доля серебра выше, чем должна быть.
1. Расчет:
m2 = 20´0,75-9.9=5.1 кг;
m1 = 9.9-5.1 = 4.8 кг
Таким образом, изделие содержит 4.8 кг золота и 5.1 кг серебра и, следовательно, ювелир похитил 3.2 кг золота (заменив их 3.2 кг серебра).
2. Анализ реальной погрешности измерения и запись результата измерения.
 ,
,  ,
, 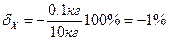 .
.
Выводы:
1.Таким образом, погрешность измерения веса короны в воздухе не превышает заданную предельно допустимую погрешность (2%).
2. Ювелир обманул царя, присвоив 3.2 кг золота, заменив эту массу серебром.
Это пример простейшей МВИ, в этом эксперименте не учитываются многочисленные факторы, влияющие на погрешность эксперимента. При заданной достаточно большой погрешности (2%) в этом не было необходимости. Но если бы от экспериментатора потребовали существенного снижения погрешности измерений, МВИ существенно бы изменилась (пример эталонного взвешивания Д.И. Менделеевым). В качестве одной из составляющих суммарной погрешности измерений является неучтенная систематическая погрешность. В нашем опыте, проведенном во времена Архимеда о многих составляющих погрешности, особенно систематических погрешностях, просто не знали или не считали их важными. Например, удельный вес золота брался равным 200 ед. (точное значение – 196,97), а серебра – 100 ед. (точное значение – 107, 87).
Подсчитаем неучтенную систематическую погрешность от этого фактора.
Пусть ювелир будет абсолютно честным человеком.
Подставим в формулу (1) истинные значения удельного веса золота и серебра, известные нам, но не известные даже Архимеду. При этом будем считать, что исходное количество золота (8кг) и серебра (2кг) измерены точно. (Архимед уже умел достаточно точно измерять веса). Получим результат:
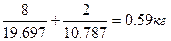
Он отличается от рассчитанного выше на 0.01кг. Сразу отметим, что столь малая систематическая ошибка вызвана тем, что удельный вес золота Архимед брал чуть выше нормы (200), а серебра – чуть ниже (100). В результате произошла небольшая компенсация систематических ошибок.
Пусть в результате опыта Архимед получил именно это число – о.59кг. Подставим это число в формулы (2) и (3):


Результат АРХИМЕДА БЫ УДИВИЛ: ЮВЕЛИР ДОБАВИЛ В КОРОНУ СВОЕГО ЗОЛОТА 200гр, а серебра – уменьшил на это же количество.
А теперь возьмем вариант такой: ювелир был очень высоким профессионалом и как алхимик владел точными знаниями удельных весов драгоценных металлов (которые он конечно же держал в секрете). Ему ничто не стоило добиться такого соотношения золота и серебра в короне, чтобы разница ее весов в воздухе и воде была точно равна ожидаемой Архимедом, т.е. 0.6кг.
Сколько золота оставил ювелир в короне при этом?
 кг, отсюда
кг, отсюда  ;
;  кг.
кг.
Таким образом, ювелир спокойно может присвоить 201 грамм золота, не вызывая подозрения у великого Архимеда, а значит и царя!
Вот что такое грамотная МВИ!
Здесь мы подходим к вопросу: а какой точностью эксперимента необходимо задаваться? Необходимо осознавать, что проведение высокоточных измерений – дорогостоящая операция. Чем точнее прибор, тем он дороже и сложнее его эксплуатация (поверка, проведение измерения и т.д.). Предельная по сложности и дороговизне задача в этой области – сличение эталонов или разработка новых эталонов.
Одно из определений: эталон есть конкретное воспроизведение единицы с наивысшей точностью (М.Ф. Маликов). Это не совсем корректное определение. Точность эталона должна быть достаточной для поверки основного парка средств измерения в стране. Точность обходится очень дорого и никто не создает суперточный эталон при отсутствии потребности в такой точности измерений. Уместно отметить, что каждая страна имеет свои национальные первичные эталоны всего в одном экземпляре, т.к. их разработка и содержание обходятся в значительные суммы.
Разработка новых эталонов (как правило, на новых физических принципах) производится на основании потребности науки или промышленности.
Самым точным является эталон единицы времени и частоты. Роль этих эталонов в мировой метрологической практике всегда была очень высокой.
До 1967 года использовались естественные эталоны времени  -периоды вращения Земли вокруг оси и вокруг солнца (
-периоды вращения Земли вокруг оси и вокруг солнца ( ). Такую же точность имели и лучшие маятниковые часы. Развитие науки и техники (астронавигация, космонавтика, радиоэлектроника и др.) потребовали более точные СИ, а, следовательно, и новые эталоны. С 1967 года секунда стала определяться как интервал времени, в течение которого совершается 9192631770 периодов излучения, соответствующих переходу между двумя уровнями сверхтонкой структуры основного состояния атома цезия-133 (
). Такую же точность имели и лучшие маятниковые часы. Развитие науки и техники (астронавигация, космонавтика, радиоэлектроника и др.) потребовали более точные СИ, а, следовательно, и новые эталоны. С 1967 года секунда стала определяться как интервал времени, в течение которого совершается 9192631770 периодов излучения, соответствующих переходу между двумя уровнями сверхтонкой структуры основного состояния атома цезия-133 ( ). Хороший скачок! Но сегодня этой точности науке и технике не хватает. Ведется разработка новых реперов с названием «Фонтан». Ожидаемая погрешность
). Хороший скачок! Но сегодня этой точности науке и технике не хватает. Ведется разработка новых реперов с названием «Фонтан». Ожидаемая погрешность  . Уже работают 6 «Фонтанов» (США, ФРГ, Франция, Канада, Япония и Южная Корея). На очереди – российский эталон. (Стоимость разработки ~1 млн. долларов).
. Уже работают 6 «Фонтанов» (США, ФРГ, Франция, Канада, Япония и Южная Корея). На очереди – российский эталон. (Стоимость разработки ~1 млн. долларов).
На втором месте – эталон длины (до  ). Опять же потребность науки и техники: микроэлектроника (размеры транзисторов на ЧИПе), нанотехнологии.
). Опять же потребность науки и техники: микроэлектроника (размеры транзисторов на ЧИПе), нанотехнологии.
А вот точность единицы силы света – канделы в  раз меньше точности эталона времени. В чем дело? Просто нет необходимости в измерениях такой точности.
раз меньше точности эталона времени. В чем дело? Просто нет необходимости в измерениях такой точности.
Дело в том, что световые измерения -это измерения «видимого» света с длиной волны от 0.38 до 0.76 мкм и в значительной степени связаны с ощущением человека, воспринимающего световой поток посредством глаза. Поскольку чувствительность глаза к разным длинам волн неодинакова, то эти измерения не совсем объективны. Это область фотометрии (фотография, кино и т.п.), поэтому и не нужна здесь запредельная точность. Ведь за точность нужно платить и платить очень дорого. Поэтому никто не занимается увеличением точности эталонов исходя только из научной любознательности.
Третье место по точности занимает эталон единицы массы (килограмма). Это один из немногих оставшихся рукотворных эталонов. Его прототип в виде платино-иридиевой гири существует с 1889 года. Случай уникальный. Всего в мире существует 42 прототипа килограмма (в России – два эталона, тоже уникальное явление). Их погрешность порядка  . Нанотехнологии требуют повышения точности измерения не только размеров, но и массы.
. Нанотехнологии требуют повышения точности измерения не только размеров, но и массы.
Много лет шли поиски более точного способа воспроизводства единицы массы. Были неоднократные попытки воспользоваться постоянной Авогадро Na –фундаментальной физической константой (число молекул или атомов в 1 моле вещества; Na=6.022* моль
моль ),которая связывает единицу массы (килограмм) с атомной массой:
),которая связывает единицу массы (килограмм) с атомной массой:
1кг=( ) Na*1а.е.м.
) Na*1а.е.м.
До последнего времени погрешность измерения Na составляла ~ (как и у гири), но пользоваться старым эталоном было гораздо проще!
(как и у гири), но пользоваться старым эталоном было гораздо проще!
Несколько лет назад был утвержден международный проект по экспериментальному уточнению числа Авогадро (проект «Авогадро»). Его задачей ставилось определение Na с минимальной погрешностью 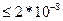 , что в 15 раз точнее физического эталона (гири).И только в 2010 году, ученые смогли справиться с этой задачей. И это были россияне (!), ученые из знаменитого Росатома. Была решена задача путем подсчета массы определенного числа атомов изотопа кремния-28 и при этом достигнуты рекордные показатели, превышающие проектное задание:
, что в 15 раз точнее физического эталона (гири).И только в 2010 году, ученые смогли справиться с этой задачей. И это были россияне (!), ученые из знаменитого Росатома. Была решена задача путем подсчета массы определенного числа атомов изотопа кремния-28 и при этом достигнуты рекордные показатели, превышающие проектное задание:
*изотопная чистота кремния-28…..в 10 раз
*химическая чистота………………..на 50%.
По прогнозам специалистов новая константа Авогадро будет утверждена до конца 2010 года, что позволит перейти на новый эталон массы: выигрыш по точности- почти два порядка!
1.2. Средства измерения и их свойства.
Классификация СИ:
*Меры – средства измерения, предназначенные для воспроизведения физической величины заданного размера;
* Измерительные преобразователи – СИ, предназначенные для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и (или) хранения, но не поддающиеся непосредственному восприятию наблюдателем;
* Измерительные приборы – средства измерения, предназначенные для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем;
* Измерительные установки – совокупность функционально объединенных СИ и вспомогательных устройств, предназначенная для выработке сигналов измерительной информации в форме, удобной для непосредственного восприятия наблюдателем и расположенная в одном месте;
* Измерительная система (информационно-измерительная система) – совокупность СИ, ЭВМ и вспомогательных устройств, соединенных между собой каналами связи, предназначенная для выработки сигналов измерительной информации в форме, удобной для их автоматической обработки, передачи и хранении.
1.3. Метрологические характеристики СИ.
Технические характеристики СИ, оказывающие влияние на результаты и погрешности измерений, называются метрологическими характеристиками (МХ). От точности характеристик при изготовлении СИ, стабильности их в процессе эксплуатации зависит точность результатов измерения.
Важнейшей метрологической характеристикой СИ является погрешность СИ, которая определяет, насколько действительные свойства СИ близки к номинальным.
Следует различать четыре составляющие погрешности СИ:
· основная;
· дополнительная;
· обусловленная взаимодействием СИ и объекта измерения;
· динамическая.
Основная погрешность – обусловлена неидеальностью собственных свойств СИ. Выражается в виде класса точности СИ.
Погрешность может выражаться различными способами.
 |
Абсолютная погрешность выражается в единицах измеряемой величины.
D = Х – Аи ,
где: D - абсолютная погрешность (в единицах измеряемой ФВ)
Х – результат измерения
Аи – истинное значение измеряемой ФВ.
На практике, абсолютную погрешность определяют по формуле:
D = Х – А ,
,
где  – действительное значение измеряемой ФВ.
– действительное значение измеряемой ФВ.
По такой погрешности нельзя напрямую судить о точности измерения.
Пример:
В результате эксперимента получили: D = 10. мВ.
Если измеряемое напряжение Uх = 1000 В, то точность измерения можно считать высокой, а если Uх = 1 В – низкой.
Для оценки точности измерений более удобно пользоваться относительной погрешностью.
Относительная погрешность – это отношения абсолютной погрешности измерения к истинному (действительному) значению измеряемой величины:
 ,
,
Где А - действительное значение ФВ.
- действительное значение ФВ.
Относительная погрешность чаще выражается в процентах:  .
.
Для указания и нормирования погрешности средства измерения (СИ), используется еще один способ выражения погрешности – приведенная погрешность.
Приведенная погрешность – это относительная погрешность, в которой абсолютная погрешность СИ отнесена к условно принятому нормирующему значению ХN, постоянному во всем диапазоне измерений (или части диапазона).
 или
или 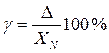
В качестве нормирующего значения ХN принимают:
§ В стрелочных (аналоговых) приборах ХN = Хк, где Хк – верхний предел измерений данного СИ, у которого начальное значение равно «0».
 |
Рис.
Шкалы приборов
Если значение «0» находится в середине шкалы, то ХN = |-Х1| + Х2 (рис.).
§ Для СИ, шкала которых имеет условный нуль, ХN равно модулю разности пределов измерений.
Например, шкала термоэлектрического термометра имеет градуировку «1000¸6000С». Для него Хn=5000С.
Пример 2: Медицинский ртутный термометр имеет шкалу: «350¸420С».
ХN= 420-350= 70С.
§ В цифровых измерительных приборах (ЦИП) нормирующее значение ХN указывается в технических характеристиках прибора для каждого поддиапазона (в таблице).
Классы точности СИ.
Метрологические характеристики, введенные ГОСТ 8.009-84, наиболее полно описывают метрологические свойства СИ. На практике, однако, чаще всего используются метрологические характеристики, которые нормируются на основе классов точности.
Класс точности --это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности позволяет судить о том, в каких пределах находится погрешность СИ данного типа.
Пределы допускаемых основной и дополнительных погрешностей выражают в форме абсолютных, относительных и приведенных погрешностей. Выбор формы представления зависит от характера изменения погрешности в пределах диапазона измерений, а также от условий применения и назначения СИ.
1. Пределы допускаемой абсолютной основной погрешности устанавливаются по одной из формул:

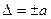 или
или  , где x -значение измеряемой величины;
, где x -значение измеряемой величины;  и
и 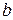 - положительные числа, не зависящие от
- положительные числа, не зависящие от  . Первая формула описывает чисто аддитивную погрешность (не зависящую от измеряемой величины), а вторая – сумму аддитивной и мультипликативной (зависящей от
. Первая формула описывает чисто аддитивную погрешность (не зависящую от измеряемой величины), а вторая – сумму аддитивной и мультипликативной (зависящей от  ) погрешностей.
) погрешностей.
В этом случае в технической документации класс точности обозначают буквами латинского алфавита или римскими цифрами (пригодились).
Например "Класс точности М".
2. Пределы допускаемой относительной основной погрешности:
а). При отсутствии мультипликативной составляющей:
 , если
, если  .
.
Обозначение класса точности на приборе в виде  ®,где R-числовое значение из ряда q.
®,где R-числовое значение из ряда q.
б). При наличии мультипликативной погрешности:
 .
.
Класс точности обозначается в виде "c/d"
в). Пределы допускаемой приведенной основной погрешности:
 , где
, где  -нормирующее значение.
-нормирующее значение.
Класс точности обозначают конкретным числом "p", например 0.5.
В приведенных формулах  --отвлеченные положительные числа, выбираемые из параметрического ряда: (1;1.5;2;2.5;4;5;6)
--отвлеченные положительные числа, выбираемые из параметрического ряда: (1;1.5;2;2.5;4;5;6) , где n=1;0;-1;-2;...
, где n=1;0;-1;-2;...
В обоснованных случаях пределы допускаемой относительной погрешности определяют по более сложным формулам, либо в виде графиков или таблиц.
Класс точности конкретного СИ (прибора) позволяет экспериментатору уже до проведения опыта оценить ожидаемую предельно допустимую погрешность измерения. Это очень важная составляющая раздела: планирование эксперимента.
Пример 1.
Отсчет по равномерной шкале вольтметра с начальной нулевой отметкой и предельным значением 100 Вольт составил 40 Вольт.
1. Класс точности обозначен значком  , т.е. выражается через относительную погрешность:
, т.е. выражается через относительную погрешность:
Предел ожидаемой допускаемой погрешности измерения напряжения равен:
 ,
,  .
.
Окончательная запись результата измерения:  .
.
Что означает эта запись?
Истинное значение измеряемой величины  мы не знаем, но можем утверждать, что с вероятностью Р (в данном случае Р
мы не знаем, но можем утверждать, что с вероятностью Р (в данном случае Р 0.997) оно находится в заданном интервале (доверительном интервале).
0.997) оно находится в заданном интервале (доверительном интервале).
2. Класс точности обозначен значком 0.5, т.е. выражается через приведенную погрешность:
Предел ожидаемой допускаемой погрешности измерения
равен:  ,
, 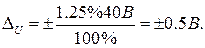
Окончательная запись результата измерения: 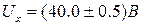 .
.
Б). Дополнительная погрешность.
Для каждого СИ в нормативно-технических документах оговариваются условия эксплуатации – совокупность влияющих величин (температура окружающей среды, влажность, давление и др.), при которых нормируется его погрешность. Дополнительной называется погрешность СИ, возникающая вследствие отклонения какой-либо из влияющих величин.
Пример.
В). Погрешность, обусловленная влиянием СИ на объект исследования.
Любое СИ в простейшем случае (при измерении постоянных сигналов или переменных сигналов низкой частоты – до сотен килогерц) может быть представлено в виде активного эквивалентного сопротивления  .
.
Для СИ, подключаемых параллельно исследуемому участку электрической цепи (например, нагрузке), это сопротивление равно входному сопротивлению прибора и указывается в инструкции (вольтметры, осциллографы и др.). При подключению такого прибора к схеме (нагрузке), параметры электрической цепи меняются и мы получаем дополнительную погрешность – систематическую методическую погрешность. Систематическая – т.к. она всегда постоянна, а «методическая» - поскольку обусловлена методом измерения.
Чем больше входное сопротивление прибора, тем меньше его влияние на исследуемую электрическую схему: методическая погрешность меньше!
Пример.
Иначе влияют на исследуемую схему СИ, включаемые последовательно с нагрузкой (например, при измерении тока в нагрузке). Они обладают внутренним активным сопротивлением, которое включается последовательно с нагрузкой. Чем меньше внутреннее сопротивление прибора, тем меньше его влияние на исследуемую схему.
Пример.
Г). Динамическая погрешность – погрешность СИ, возникающая при измерении изменяющейся (в процессе измерений) физической величины, являющаяся следствием инерционных свойств СИ.
Схема любого электронного прибора содержит реактивные элементы: конденсаторы С, индуктивности L, в том числе и паразитные. Даже при подключении СИ, например вольтметра, к источнику постоянного тока, процесс установления показания прибора является конечным: пока не зарядятся все конденсаторы. Этим и обусловлены инерционные свойства электронных приборов. Верные показания будут только при установившемся режиме. Теоретически процесс зарядки конденсатора бесконечен (конденсатор заряжается по экспоненциальному закону), а практически для каждого прибора задается (в паспортных данных) время установления, после которого можно снимать показания с допустимой динамической погрешностью.
Для электромеханических приборов (ЭМП) время установления может составлять 4-6 секунд. У цифровых приборов оно существенно меньше
(микро-, наносекунды и меньше).
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 705; Нарушение авторских прав?; Мы поможем в написании вашей работы!