Пространственная система сил

Решение задач на равновесие плоской системы сил

Для решения задач на равновесие плоской системы сил можно пользоваться любой формой уравнений равновесия, приведенной в § 19. Составляя уравнения равновесия, следует учитывать, что мы имеем полную свободу выбора координатных осей и центров моментов. Эту свободу выбора нужно разумно использовать для упрощения вычислений, связанных с решением уравнений равновесия.

Целесообразно составлять уравнения так, чтобы они могли быть решены наиболее просто и быстро. Просто решается система уравнений равновесия, каждое из которых содержит одну из неизвестных. К такой системе можно прийти соответствующим выбором направления координатных осей и центра моментов.

В качестве центра моментов рекомендуется выбирать точку, где пересекаются две неизвестные силы; уравнение моментов относительной этой точки будет содержать только одну неизвестную. Направление координатных осей х и у следует выбирать так, чтобы оси были перпендикулярны некоторым неизвестным силам. При составлении уравнений проекций неизвестные, перпендикулярные соответствующей оси, в эти уравнения не войдут.

Определение неизвестных величин лучше начинать с уравнений моментов, а затем переходить к уравнениям проекций. При этом можно избежать совместного решения уравнений и, следовательно, уменьшить вероятность ошибок.

Следует отметить еще один важный момент. Для плоской системы сил можно выбрать любое число осей проекций и любое число центров моментов. Проектируя силы данной плоской системы на различные оси и составляя уравнения моментов относительно любых точек, можно написать сколько угодно уравнений равновесия, но только три из них будут независимыми. Остальные уравнения являются следствием этих трех уравнений и могут служить лишь для проверки решения.

Система сил называется пространственной, если линии действия сил, приложенных к телу, не лежат в одной плоскости. Подобно плоской системе пространственную систему сил можно привести к любой точке пространства. Порядок приведения тот же, что и для плоской системы сил, при этом от каждой силы в центре приведения получаем силу и пару сил.

Геометрическая сумма всех сил данной пространственной системы называется главным вектором. Модуль главного вектора определится через проекции на координатные оси х, у и z всех сил системы

R = 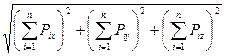. (26)

В отличие от плоской системы сил моменты сил пространственной системы относительно точки приведения действуют в разных плоскостях. Поэтому главный момент пространственной системы сил определяется как геометрическая сумма моментов всех сил относительно точки приведения.

Абсолютная величина главного момента заданной системы сил относительно некоторой точки определяется по формуле

M = 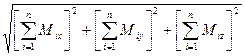, (27)

где , , 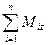– алгебраические суммы моментов всех сил системы относительно осей х, у, z, проходящих через рассматриваемую точку.

Равновесие пространственной системы сил имеет место, когда главный вектор и главный момент равны нулю, т.е.

R = 0; M = 0. (28)

На этом основании можно написать шесть уравнений равновесия:

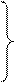
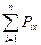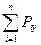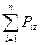= 0; = 0; =0

= 0; = 0; 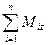= 0. (29)

Глава V

Дата добавления: 2014-01-07