Центры тяжести площадей. Статические моменты площадей

Во многих задачах приходится определять центры тяжести различных сочетаний тел, представляющих собой геометрические плоские фигуры иногда весьма сложной формы. Рассмотрим плоскую однородную пластинку (рис. 25). Вес каждой ее части P_i будет пропорционален ее площади F_i. Обозначим γ - вес одного квадратного метра пластинки, тогда

P_i = γ F_i.

Разделив числитель и знаменатель в формулах (31) на γ, получим формулу для определения координат центра тяжести плоской фигуры в ее плоскости:

х_c = 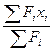; 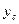= , (33)

где F_i - площади отдельных частей фигуры; х_i, y_i - координаты центров тяжести этих частей.

Рис. 25

Произведение части площади F_i фигуры (рис. 25) на расстояние от ее центра тяжести до какой либо оси называется статическим моментом этой части площади относительно данной оси. Так, статический момент площади F_i относительно оси х будет S_ix= F_iy_i, а относительно оси y будет S_iy= F_ix_i.

Сумма статических моментов всех частей фигуры называется статическим моментом площади фигуры относительно данной оси:

S_x= = ;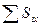

= = .

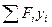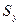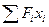Размерность статического момента площади выражается единицами длины в третьей степени, т.е., L³ или, например, см³, мм³, м³.

Координаты центра тяжести плоской фигуры можно выразить через статические моменты площадей. В общем виде, если какая – либо сложная фигура, площадь которой равна F, разделена на несколько простых частей, то

X_c = 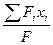= ; 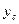= = 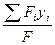. (34)

Если начало координат расположить в центре тяжести площади, то статические моменты относительно осей х и у, проходящих через центр тяжести, будут равны нулю, так как в этом случае у_с = 0 и х_с = 0.

Следовательно, статический момент плоской фигуры относительно любой центральной оси равен нулю.

В заключение приведем (без выводов) сведения о координатах центров тяжести некоторых простых фигур, которые могут встретиться при решении задач.

Рис. 26

Центр тяжести параллелограмма, а также прямоугольника и квадрата совпадает с точкой С пересечения диагоналей (рис. 26, а). Центр тяжести треугольника лежит на пересечении медиан (рис. 26, б). Положение центра тяжести кругового сектора (рис. 26, в) определяют по формуле 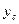(35)

=, (35)

где a - центральный угол сектора в радианах.

Положение центра тяжести сегмента круга (рис. 26, г) определяют по формуле 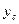(36)

= . (36).

Дата добавления: 2014-01-07