Методы анализа основной тенденции развития в рядах динамики

Одна из важнейших задач статистики – определение в рядах динамики тенденции развития

Основной тенденцией развития называется плавное и устойчи­вое изменение уровня явления во времени, свободное от случайных колебаний. Задача состоит в выявлении общей тенденции в измене­нии уровней ряда, освобожденной от действия различных факторов.

Изучение тренда включает два основных этапа:

· ряд динамики проверяется на наличие тренда;

· производится выравнивание временного ряда и непосред­ственное выделение тренда с экстраполяцией полученных ре­зультатов.

С этой целью ряды динамики подвергаются обработке мето­дами укрупнения интервалов, скользящей средней и аналитиче­ского выравнивания:

1. Метод укрупнения интервалов.

Одним из наиболее элементарных способов изучения общей тенденции в ряду динамики является укрупнение интервалов. Этот способ основан на укрупнении периодов, к которым отно­сятся уровни ряда динамики. Например, преобразование месяч­ных периодов в квартальные, квартальных в годовые и т. д.

2. Метод скользящей средней.

Выявление общей тенденции ряда динамики можно произвести путем сглаживания ряда динамики с помощью скользящей средней.

Скользящая средняя - подвижная динамическая средняя, которая рассчитывается по ряду при последовательном передви­жении на один интервал, то есть сначала вычисляют средний уровень из определенного числа первых по порядку уровней ря­да, затем - средний уровень из такого же числа членов, начиная со второго. Таким образом, средняя как бы скользит по ряду ди­намики от его начала к концу, каждый раз отбрасывая один уро­вень в начале и добавляя один следующий.

При этом посредством осреднения эмпирических данных ин­дивидуальные колебания погашаются, и общая тенденция разви­тия явления выражается в виде некоторой плавной линии (теоре­тические уровни). Итак, суть метода заключается в замене абсо­лютных данных средними арифметическими за определенные периоды.

Скользящая средняя обладает достаточной гибкостью, но не­достатком метода является укорачивание сглаженного ряда по сравнению с фактическим, что ведет к потере информации. Кро­ме того, скользящая средняя не дает аналитического выражения тренда.

Период скользящей может быть четным и нечетным. Прак­тически удобнее использовать нечетный период, так как в этом случае скользящая средняя будет отнесена к середине периода скольжения. Скользящие средние с продолжительностью перио­да, равной 3, следующие:

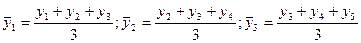и т.д.

Полученные средние записываются к соответствующему срединному интервалу.

Особенность сглаживания по четному числу уровней состоит в том, что каждая из исчисленных (например, четырехчленных) средних относится к соответствующим промежуткам между смежными периодами. Для получения значений сглаженных уровней соответствующих периодов необходимо произвести цен­трирование расчетных средних.

Недостатком способа сглаживания рядов динамики является то, что полученные средние не дают теоретических рядов, в ос­нове которых лежала бы математически выраженная закономер­ность.

3. Метод аналитического выравнивания.

Более совершенным приемом изучения общей тенденции в рядах динамики является аналитическое выравнивание. При изу­чении общей тенденции методом аналитического выравнивания исходят из того, что изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены определенными математическими функциями. Вид уравнения определяется характером динамики развития конкретного явле­ния. Логический анализ при выборе вида уравнения может быть основан на рассчитанных показателях динамики, а именно:

если относительно стабильны абсолютные приросты (пер­вые разности уровней приблизительно равны), сглаживание мо­жет быть выполнено по прямой;

· если абсолютные приросты равномерно увеличиваются (вторые разности уровней приблизительно равны), можно при­нять параболу второго порядка;

· при ускоренно возрастающих или замедляющихся абсолютных приростах - параболу третьего порядка;

· при относительно стабильных темпах роста - показательную функцию.

Для аналитического выравнивания наиболее часто использу­ются следующие виды трендовых моделей: прямая (линейная), парабола второго порядка, показательная (логарифмическая) кри­вая, гиперболическая.

Цель аналитического выравнивания - определение аналити­ческой или графической зависимости. На практике по имеюще­муся временному ряду задают вид и находят параметры функции, а затем анализируют поведение отклонений от тенденции. Чаще всего при выравнивании используются следующие зависимости: линейная, параболическая и экспоненциальная.

После выяснения характера кривой развития необходимо опре­делить ее параметры, что можно сделать различными методами:

1) решением системы уравнений по известным уровням ряда динамики;

2) методом средних значений (линейных отклонений), кото­рый заключается в следующем: ряд расчленяется на две пример­но равные части, и вводятся преобразования, чтобы сумма вы­равненных значений в каждой части совпала с суммой фактиче­ских значений, например, в случае выравнивания прямой линии

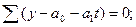
3) выравниванием ряда динамики с помощью метода конечных разностей;

4) методом наименьших квадратов: это некоторый прием по­лучения оценки детерминированной компоненты f(t), характери­зующий тренд или ряд изучаемого явления.

Во многих случаях моделирование рядов динамики с помощью полиномов или экспоненциальной функции не дает удовле­творительных результатов, так как в рядах динамики содержатся заметные периодические колебания вокруг общей тенденции. В таких случаях следует использовать гармонический анализ.

Вывод по 1-му вопросу: Изменение социально-экономических явлений во времени изучается статистикой методом построения и анализа динамических рядов. Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности. Каждый динамический ряд содержит две составляющие: 1) показатели периодов времени (годы, кварталы, месяцы, дни или даты); 2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда.

Дата добавления: 2014-01-07