Структурні середні в статистиці

Тема 5. АНАЛІЗ РЯДІВ РОЗПОДІЛУ

Як було визначено раніше, середня є узагальненим показником сукупності, що вивчається. Але середня не дуже часто співпадає з окремими варіантами. Тому виникає потреба розглянути конкретні значення варіант, які займають в упорядкованій сукупності значення ознак певне місце.

До характеристик центру розподілу належать мода та медіана.

Мода (Мо) ― варіанта, яка найчастіше повторюється в ряді розподілу, або та ознака, яка має найбільшу частоту.

У дискретному ряді моду легко відшукати, знаючи її визначення.

У інтервальному ряді спочатку треба відшукати модальний інтервал, а мода буде визначена за формулою:

, (5.1)

Де ― нижня межа модального інтервалу;

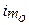― ширина модального інтервалу;

― частота модального інтервалу;

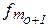; ― частота попереднього і наступного інтервалу відносно модального.

Медіана (Ме) ― це варіанта, що ділить ранжирований ряд на дві рівні частини.

Якщо парне число варіант записане в порядку зростання чи зменшення, то медіана розраховується як середня арифметична двох центральних варіант, а коли непарне ― то центральна варіанта буде медіаною.

Пошук центральної варіанти можливо полегшити за допомогою кумулятивних частот.

У дискретному ряді медіану визначають за кумулятивними частотами.

Для цього насамперед встановлюють порядковий номер центральної варіанти.

У інтервальному ряді розподілу аналогічно визначається медіанний інтервал, а сама медіана обчислюється за формулою:

, (5.2)

Де 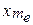― нижня межа медіанного інтервалу;

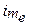― ширина медіанного інтервалу;

― кумулятивна частота інтервалу, що передує медіанному;

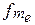― частота медіанного інтервалу.

Мода і медіана ― особливий вид середніх величин, вони завжди збігаються з конкретними варіантами, на них не впливають значення варіант, не характерних для даної сукупності.

Якщо , то сукупність вважають однорідною, а розподіл симетричним.

5.2 Характеристика показників варіації

Як загальний показник для всіх одиниць статистичної сукупності, середня величина не завжди дає уявлення про індивідуальні значення варіюючих ознак та про розходження поміж ними. Середня величина гасить коливання ознаки, що вивчається, у окремих одиниць сукупності.

Для повної характеристики сукупності недостатнім є використання тільки середньої величини.

З цією метою в статистиці розраховують: розмах варіації, середнє лінійне відхилення, дисперсію, середнє квадратичне відхилення та коефіцієнт варіації.

Самим простим показником, який характеризує коливання ознаки є розмах варіації (R). Він розраховується як відхилення поміж максимальним та мінімальним значеннями ознаки у варіаційному ряді:

(5.3)

Середнє лінійне відхилення () ― середня арифметична з абсолютних

значень відхилень окремих варіант від їх середньої. Якщо кожна з варіант зустрічається в сукупності тільки один раз, то:

, (5.4)

де ― абсолютне значення відхилення окремих варіант від їх середньої арифметичної;

n― кількість членів ряду.

Для варіаційного ряду з різними частотами формула має вигляд:

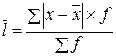, (5.5)

де f ― частота варіаційного ряду.

Дисперсія () ― середній квадрат відхилень варіант від їх середньої арифметичної.

Якщо має місце відсутність частот або їх однакова кількість, розраховують просту дисперсію:

, (5.6)

якщо кожен варіант має свою частоту, то розраховують зважену дисперсію:

(5.7)

У економіко-статистичному аналізі варіацію ознак частіше оцінюють за середнім квадратичним відхиленням (σ), що являє собою корінь з дисперсії:

(5.8)

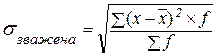(5.9)

У статистичній практиці дуже часто виникає необхідність порівняння варіацій різних ознак. Середнє лінійне та середнє квадратичне відхилення є мірою абсолютного коливання ознаки і завжди мають бути виражені в тих же одиницях, що й ознака, яку вивчають. Це не дозволяє порівнювати поміж собою середні відхилення різних показників. Наприклад, порівняння варіацій стажу роботи в роках та розміру їх заробітної плати в гривнях; віку робітників та їх кваліфікації.

Вихід з такого становища можна знайти використовуючи показник варіації ― коефіцієнт варіації (ν):

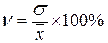(5.10)

Дата добавления: 2014-01-07