Системы счисления и математические операции с двоичными числами

Кодирование сигналов

Лекция № 4

Методика построения кодов тесно связана с соответствующими системами счисления.

В основе любой системы счисления лежит основание системы, т.е. то количество цифр, из комбинаций которых можно получить любое число.

Так, сущность десятичной системы счисления заключается в том, что, располагая десятью цифрами (от 0 до 9), мы можем записать любое из чисел. Десять – уже двузначное число, которое записывается единицей в разряде десятков и нулём в разряде единиц. По этому принципу можно построить систему счисления из любого числа цифр.

В основу двоичной системы положены лишь два числа 0 и 1. Десятичное число 2 передаётся как 10. Число 3→2+1, т.е. 10+1=11. Число 2² = 4 представляется как (10²)=100. Число 5=4+1 т.е. 100+1=101 и т.д.

Широко используемая десятичная система имеет слишком много цифр для запоминания и воспроизведения. Восьмеричная система счисления применяется при составлении программ, т.к. запись по ней примерно в 3 раза короче, чем по двоичной (2³=8).

Двоичная система счисления нашла широкое применение в вычислительной технике, где из-за применения в ней только двух цифр (0 и 1) просто осуществляются арифметические операции. Схемная реализация операции с двоичными числами производится без всяких затруднений, что объясняется тем, что многие устройства, используемые в вычислительной технике и телемеханике, являются устройствами релейного действия (электромеханические и бесконтактные реле, триггеры, лампы тлеющего разряда, магнитные элементы с прямоугольной петлёй гистерезиса и др.), обладают двумя устойчивыми состояниями, соответствующими 1 или 0.

Перевод десятичного числа в двоичное и обратно. Для этого десятичное число делят на два, остаток записывают, а полученное частное снова делят на 2. Далее остаток снова записывают, а частное вновь делят на 2. Деление на два продолжается до тех пор, пока частное не станет равно 1. Эта 1 и полученные остатки выписываются и образуют двоичное число, которое соответствует десятичному. Например, переведём число 29

Делимое Делитель Частное Остаток

29 2 14 1

14 2 7 0

7 2 3 1

3 2 3 1

В итоге получим число 11101, которое записываем так: сначала последняя единица частного, а затем все остатки, начиная снизу.

Для перевода двоичного числа в десятичное нужно удваивать числа, начиная со старшего разряда, придерживаясь следующих правил: 1) если в следующем разряде стоит нуль, то число только удваивается; 2) если в следующем разряде стоит единица, то число удваивается и к нему прибавляется ещё единица. Эта процедура проделывается только до разряда десятков включительно. Переведём числа 11101. Первую единицу удвоим и, прибавив к результату 1, получим 3. Далее удвоим 3 и, прибавив 1, получим 7. Удвоим 7, получим 14. И, наконец, удвоив 14 и прибавив 1, получим в итоге 29, т.е.

1 1 1 0 1

3 7 14 29

Перевод можно получить также путём подписывания под двоичным числом его десятичного эквивалента. Далее производится суммирование всех разрядов в десятичном эквиваленте, в которых стоит единица. Например, число 53

1 1 0 1 0 1

2⁵ 2⁴ 2³ 2² 2¹ 2⁰

32 + 16 + 8 + 4 + 2 + 1 = 53

Запись кодовых комбинаций в виде многочлена. Любое число в системе счисления с основанием Х можно представить в виде многочлена.

Так n – разрядное число запишется:

F(X) = a_n-1X^n-1+a_n-2X^n-2+……+ a₁X¹+a₀X⁰, где а – это цифровые знаки, имеющие значение от 0 до Х-1.

В десятичной системе счисления Х=10, а – это цифры 0,1,2,….,9. Например, четырёхзначное число 4357 запишется:

F(10)=4∙10³+3∙10²+5∙10¹+7∙10⁰=4357

т.к. n = 4 – количество цифр, т.е. число разрядов

В двоичной системе счисления, где X=2, коэффициенты a принимают только одно из двух значений: 1 или 0. Двоичное число 10101001 в десятичном эквиваленте запишется:

F(2)=1∙2⁷+0∙2⁶+1∙2⁵+0∙2⁴+1∙2³+0∙2²+0∙2¹+1∙2⁰=169

То же число 10101001 запишется в виде многочлена

Q(X)= 1∙Х⁷+0∙Х⁶+1∙Х⁵+0∙Х⁴+1∙Х³+0∙Х²+0∙Х¹+1∙Х⁰

Опуская члены с коэффициентами, равными нулю, и не выписывая единицы как множитель, получаем:

Q(X)= Х⁷+Х⁵+Х³+1.

Таким образом, члены многочленов записываются только при наличии коэффициента единицы. При этом степени соответствующего числа многочлена берётся уменьшенной на 1 по отношению к номеру разряда в двоичной записи, отсчитанному справа налево. Так, первым записывается Х⁷ несмотря на то, что этот член в двоичной записи находиться в восьмом разряде.

Сложение. Над многочленами можно производить все алгебраические операции. Обычное сложение с переносом числа в высший разряд здесь неприменимо, т.к. это может привести к образованию нового более высокого разряда, чем это принято в данном коде, что недопустимо. Поэтому применяется так называемое сложение двоичных чисел по модулю два, обозначаемое знаком

При двух слагаемых правила сложения следующие:

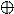
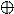
0 0=0; 0 1=1; 1 0=1; 1 1=0.

При сложении многозначных чисел складываются разряды, занимающие одинаковые места. При этом сложение сводится к сложению только коэффициентов при членах совпадающих степеней.

Дата добавления: 2014-01-07