Графические решения двумерных задач

Рассмотрение графического метода решения задач, обладающего высокой степенью наглядности, позволяет выявить некоторые общие свойства задач линейного программирования, которые указывают на пути их общего решения.

Упражнение №8. Минимизировать функцию Z=–3Х₁–4Х₂ при ограничениях X₁≥10, X₂≥5, Х₁+Х₂≤20,–Х₁+4Х₂≤20.

Графическое решение задачи на рис. 8.

Рис. 8. Область допустимых значений для упражнения № 8

Допустимой областью является четырехугольник PQRS. Функция Z убывает в направлении вектора (3,4). Минимальное значение функции Z= –68 достигается в точке R(12,8). Обратим внимание на то обстоятельство, что и как в упражнении № 7 экстремум достигается в вершине допустимой области.

В некоторых случаях задача может иметь более одного решения.

Упражнение №9. Минимизировать функцию Z= 6Х₁–2Х₂ при ограничениях X₁≥0, X₂≥0, 2Х₁+4Х₂≤9, 3Х₁+Х₂≤6.

Допустимой областью является четырехугольник OABC. Функция Z убывает в направлении вектора (2,6). С учетом этого обстоятельства любая точка на отрезке BC является оптимальным решением.

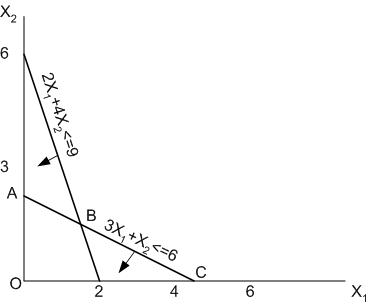
Рис. 9. Область допустимых значений для упражнения № 9

В некоторых случаях оптимальное решение не имеет ограничения.

Упражнение № 10. Максимизировать функцию Z=Х₁+Х₂ при ограничениях X₁≥0, X₂≥0, Х₁-Х₂≥1, Х₂≤2.

Рис. 10. Область допустимых значений для упражнения № 10

Допустимая область не ограничена в направлении возрастания функции Z. Решение также не ограничено.

В некоторых случаях задача может и не иметь решений, поскольку допустимой области не существует.

Упражнение №11. Минимизировать функцию Z=2Х₁+3Х₂ при ограничениях X₁≥0, X₂≥0, Х₁+Х₂≥10, 3Х₁+5Х₂≤15.

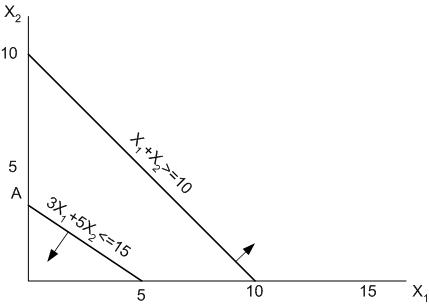
Рис. 11. Графическое решение задачи для упражнения № 11

Из рассмотренных примеров выявляются некоторые характерные особенности оптимальных решений.

1. Допустимая область решения задачи – выпуклый многоугольник, даже в случае, когда решение не имеет ограничения.

2. Оптимальное решение задачи всегда достигается в вершине (вершинах) допустимой области.

Все вышесказанное может иметь обобщения. Сначала покажем, что задачи линейного программирования могут быть приведены к стандартной форме.

Дата добавления: 2014-01-07