Библиографический список. 1. Банди, Б. Основы линейного программирования / б

1. Банди, Б. Основы линейного программирования / Б. Банди. Пер. с англ. – М.: Радио и связь, 1989. –176 с.

2. Вознесенский, В.А. Численные методы решения строительно-технологических задач на ЭВМ: учебник / В.А. Вознесенский, Т.В. Ляшенко, Б.Л. Огарков; Под ред. В.А.Вознесенского. – Киев.: Выща школа, 1989. –328 с.

3. Грачев, Ю.П. Математические методы планирования экспериментов / Ю.П.Грачев. – М.: Пищевая промышленность, 1979. – 200 с.

4. Румшиский, Л.З. Математическая обработка результатов эксперимента / Л.З. Румшиский.–М.: Наука, 1971. –192 с.

5. Дэниел, К. Применение статистики в промышленном эксперименте /К.Даниэл; пер. с англ. – М.: Изд-во Мир, 1979. – 294 с.

6. Джонсон, Н. Статистика и планирование эксперимента в технике и науке: Методы планирования эксперимента / Н. Джонсон, Ф. Лион; пер. с англ. – М.: Мир,1981 – 520 с.

7. Таблицы планов эксперимента для факторных и полиномиальных моделей: Справочник. /под ред. В.В. Налимова. – М.: Металлургия, 1982. – 752 с.

ПРИЛОЖЕНИЯ

Приложение А

Значение критерия максимального отклонения R_max

Число повторностей n	Уровень значимости q	Число повторностей n	Уровень значимости q
0,05	0,01	0,05	0,01
	1,41	1,41		2,55	2,87
	1,69	1,72		2,58	2,90
	1,87	1,96		2,60	2,93
	2,00	2,13		2,62	2,96
	2,09	2,27		2,64	2,99
	2,17	2,37		2,66	3,01
	2,24	2,46		2,68	3,03
	2,29	2,54		2,70	3,05
	2,34	2,61		2,72	3,07
	2,39	2,66		2,79	3,16
	2,43	2,71		2,85	3,22
	2,46	2,76		2,90	3,28
	2,49	2,80		2,95	3,33
	2,52	2,84		2,99	3,37

Приложение Б

Значение критерия α_т для определения грубых ошибок

Число повторностей n	Уровень значимости q
0,05	0,01
	0,941	0,988
	0,765	0,889
	0,642	0,780
	0,560	0,698
	0,507	0,637
	0,468	0,590
	0,437	0,555
	0,412	0,527
	0,392	0,502
	0,376	0,482
	0,338	0,438
	0,300	0,391
	0,281	0,367
	0,260	0,341

Приложение В

Значение критерия Стьюдента t _(P,f)

Число степеней свободы f	Уровень значимости q	Число повторностей n	Уровень значимости q
0,05	0,01	0,05	0,01
	12,71	63,66		2,20	3,11
	4,30	9,93		2,18	3,06
	3,18	5,84		2,16	3,01
	2,78	4,60		2,15	2,98
	2,57	4,03		2,04	2,75
	2,45	3,71		2,02	2,70
	2,37	3,50		2,00	2,66
	2,31	3,36		1,98	2,62
	2,26	3,25	∞	1,96	2,58
	2,23	3,17

Приложение Г

Значение критерия Кохрена G для уровня значимости q =0,05

Число дисперсий	Число степеней свободы в дисперсиях
								∞
	0,544	0,507	0,478	0,439	0,412	0,365	0,307	0,251	0,200
	0,480	0,445	0,418	0,382	0,357	0,314	0,261	0,212	0,167
	0,431	0,397	0,373	0,338	0,315	0,276	0,228	0,183	0,143
	0,391	0,360	0,336	0,304	0,283	0,246	0,202	0,162	0,125
	0,358	0,329	0,307	0,277	0,257	0,223	0,182	0,145	0,111
	0,331	0,303	0,282	0,254	0,235	0,203	0,166	0,131	0,100
	0,242	0,220	0,203	0,182	0,167	0,143	0,114	0,089	0,067
	0,192	0,174	0,160	0,142	0,130	0,111	0,088	0,068	0,050
	0,138	0,124	0,114	0,100	0,092	0,077	0,060	0,046	0,033
	0,108	0,097	0,-89	0,078	0,071	0,060	0,046	0,035	0,025
	0,077	0,068	0,062	0,055	0,050	0,041	0,032	0,023	0,017
	0,042	0,037	0,034	0,029	0,027	0,022	0,017	0,012	0,008

Приложение Д

Значение критерия Фишера F для уровня значимости q =0,05

Число степе- ней свободы строк матрицы К2	Число степеней свободы единичных повторов в строке матрицы К1
								∞
	161,4	199,5	215,7	224,6	230,2	234,0	243,9	249,0	254,3
	18,5	19,0	19,2	19,3	19,3	19,3	19,4	19,5	19,5
	10,1	9,6	9,3	9,1	9,0	8,9	8,7	8,6	8,5
	7,7	6,9	6,6	6,4	6,3	6,2	5,9	5,8	5,6
	6,6	5,8	5,4	5,2	5,1	5,0	4,7	4,5	4,4
	6,0	5,1	4,8	4,5	4,4	4,3	4,0	3,8	3,7
	5,6	4,7	4,4	4,1	4,0	3,9	3,6	3,4	3,2
	5,3	4,5	4,1	3,8	3,7	3,6	3,3	3,1	2,9
	5,1	4,3	3,9	3,6	3,5	3,4	3,1	2,9	2,7
	5,0	4,1	3,7	3,5	3,3	3,2	2,9	2,7	2,5
	4,8	4,0	3,6	3,4	3,2	3,1	2,8	2,6	2,4
	4,8	3,9	3,5	3,3	3,1	3,0	2,7	2,5	2,3
	4,7	3,8	3,4	3,2	3,0	2,9	2,6	2,4	2,2
	4,6	3,7	3,3	3,1	3,0	2,9	2,5	2,3	2,1
	4,5	3,7	3,3	3,1	2,9	2,8	2,5	2,3	2,1
	4,2	3,3	2,9	2,7	2,5	2,4	2,1	1,9	1,6
	4,1	3,2	2,9	2,6	2,5	2,3	2,0	1,8	1,5
	4,0	3,2	2,8	2,5	2,4	2,3	1,9	1,7	1,4
	3,9	3,1	2,7	2,5	2,3	2,2	1,8	1,6	1,3
∞	3,8	3,0	2,6	2,4	2,2	2,1	1,8	1,5	1,0

Примечание: таблица допускает линейную интерполяцию по аргументу К₂ и квадратическую интерполяцию по аргументу К₁ с ошибкой до 0,01.

Приложение Е

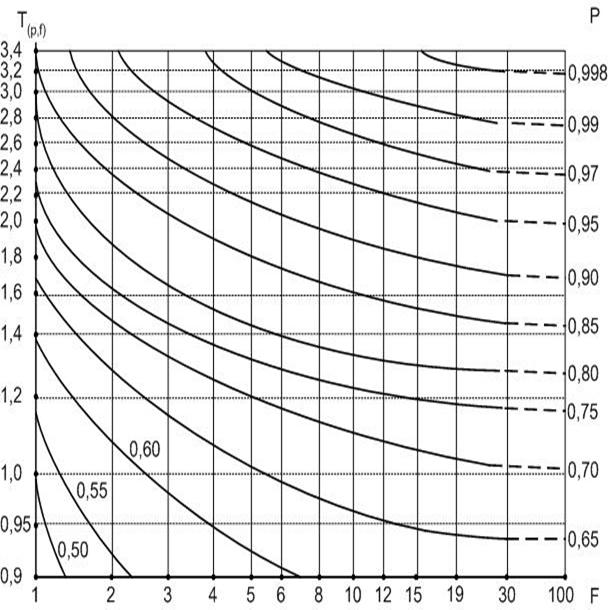
Зависимость доверительной вероятности Р от расчетного значения критерия Стьюдента t_(p,f) и числа степеней свободы f

Задачи для самостоятельной работы по разделу

«Основы линейного программирования»

Задача № 1. Фирма производит два вида продукта: воздухозащитную самоклеящуюся ленту "Герлент-М" и герметизирующую ленту "Гервасс", сбыт которых неограничен. Каждая продукция (единица измерения – рулон длиной 25 м) должна быть обработана на каждом из типов оборудования технологической линии: станках A, B, C. Время обработки в часах для каждого из изделий приведено ниже в таблице П.1.

Таблица П.1

Изделие	Тип оборудования
A	B	C
Герлент-М	0,5	0,4	0,2
Гервасс	0,25	0,3	0,4

Время работы станков в неделю соответственно составляет 40, 36 и 36 часов. Прибыль при производстве изделий составляет 150 и 200 рублей за рулон мерной длины. Определить, при каких объемах производства изделий фирма будет получать максимальную прибыль при производстве указанных выше видов продукции. Решить задачу графическим и аналитическим способами.

Задача № 2. Необходимо максимизировать функцию Z = X₁ +2 X₂ при следующих ограничениях: X₁ ≥0, X₂ ≥0, – X₁ +3 X₂ ≤0, X₁ + X₂ ≤6, X₁ – X₂ ≤3, X₁ +4 X₂ ≥4.

Ответ Максимум функции равен 10 при X₁ =2; X₂ =4.

Задача № 3. Приведите предыдущую задачу к стандартной форме. Покажите общее и допустимое количество решений. Укажите, какие из полученных решений соответствуют вершинам допустимой области.

Задача № 4. Предприятию требуется мелкий заполнитель с содержанием фракции менее 0.16 мм не более 3 % и с содержанием загрязняющий примесей не более 1 %. Возможно получение от поставщиков трех видов мелкого заполнителя: A,B и C (табл. П.2).

Таблица П.2

Вид заполнителя	Содержание фракции менее 0.16 мм	Содержание загрязняющих примесей	Стоимость 1 тонны продукта
A	6.0	0.7
B	4.1	1.3
C	2.2	1.0

Как следует смешивать виды мелкого заполнителя, чтобы получить минимальную стоимость продукта при обеспечении всех ограничений?

Задача № 5. Предприятие производит сухие смеси двух видов: А и Б, продаваемых соответственно по 40 и 75 рублей за упаковку одной массы; рынок сбыта продукции неограничен. Смесь А изготавливается в смесителе № 1, смесь В – в смесителе № 2. После этого полученные смеси фасуются на упаковочной линии «ТЕХНЕКС". Один кг сырья для смеси А стоит 30 рублей; для смеси Б 40 рублей Смеситель № 1 обрабатывает 5 т в час с потерями 2 %. Смеситель № 2 обрабатывает 4 т в час с потерями 3 %. Смеситель № 1 доступен 6 часов в день, его использование стоит 1400 рублей в час. Смеситель № 2 доступен 5 часов в день, его использование стоит 1800 рублей в час. Упаковка смеси А весит 2,50 кг, смеси Б – 3,0 кг. Предприятие может работать 10 часов в сутки, производя в 1 час продукции стоимостью 2100 рублей. За 1 час можно упаковать 12000 упаковок смеси А и 8000 упаковок смеси Б. Предприятие хочет определить, какое количество сырья для производства смесей А и Б следует закупать, чтобы его дневная прибыль была максимальна. Дать графическое решение задачи.

Задача № 6. Четыре щебеночных завода: A, B, C, D производят ежедневно соответственно 950, 300, 1350 и 450 тонн щебня фракции 10–20 мм. Щебень должен быть передан потребителям А, Б, В, Г, Д, запросы которых соответственно составляют 250, 1000, 700, 650 и 450 тонн. Стоимость транспортировки от поставщика потребителю одной тонны щебня приведена в табл. П.3.

Таблица П.3

Завод	Потребитель
А	Б	В	Г	Д
A
B
C
D

Какой нужно составить план распределения объемов перевозок, чтобы минимизировать общую стоимость.

Задача № 7. Челябинская строительная фирма предложила трем транспортным компаниям перевозить бригады строителей в различные населенные пункты области. Стоимость перевозок в тыс. руб/год. приведена в табл. П.4.

Таблица П.4

Транспортная компания	Населенный пункт Челябинской области
А	Б	В	Г	Д
A
B
C

Администрация строительной фирмы приняла решение о заключении индивидуальных контрактов с транспортными компаниями в отношении 2:3:2 и уведомила от этом менеджера фирмы, а также известила его о том, что на следующий год из 70 перевозок 10 будут осуществляться в пункт А, 15 в пункт Б, 20 в пункт В, 10 в пункт Г, 15 в пункт Д. Как менеджеру следует распределить индивидуальные контракты на перевозки для минимизации общей стоимости при условии удовлетворения запросов администрации фирмы? Какова минимальная стоимость проекта?

Таблица П.5

Транспортная компания	Населенный пункт Челябинской области
А	Б	В	Г	Д
A
B
C

Задача № 8. Герметизирующая лента производится на двух заводах и распределяется между двумя пользователями. Их потребности на ближайшие два месяца приведены в табл. П.6.

Таблица П.6

Пользователь	Потребность
апрель	май

Стоимость транспортировки готового продукта с заводов потребителям приведена в табл. П.7.

Таблица П.7

Завод	Пользователь

Стоимость производства единицы продукта и объемы производства приведены в табл. П.8.

Таблица П.8

Завод	Стоимость производства	Объем производства
	3,0	3,6
	3,2	2,9

Герметизирующую ленту можно производить в течение месяца, хранить на складе завода в течение месяца, а затем отправлять пользователю. Стоимость хранения единицы продукции на складе завода 1 составляет 0,5, на заводе 2 0,6 единиц. Требуются оптимальные планы производства и распределения продукции. Сформулируйте задачу как транспортную и найдите оптимальное решение.

Ответ: Завод 1 посылает в апреле 420 единиц продукции потребителю 1, 50 единиц - потребителю 2 и сохраняет 30 единиц продукции на май. Завод 2 посылает в апреле 300 единиц пользователю 2. Завод 1 в мае посылает пользователю 1 520 единиц текущего производства и 30 единиц со склада; завод 2 посылает 480 единиц пользователю 2.

Дата добавления: 2014-01-07