Способы представления и обработки экономических данных

Задачей статистического описания выборки является получение такого её представления, которое позволяет наглядно выявить вероятностные характеристики.

Различают следующие способы упорядочения данных: по возрастанию, по совпадающим значениям, по интервалам и т.п.

Разность между максимальным и минимальным значениями выборки называется размахом выборки: .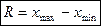

Пусть объём выборки равен n, а число различных значений k (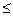 n). Тогда значения называются вариантами.

Если значение встретилось в выборке 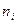раз, то число 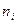называют частотой значения .

Отношение частоты 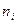к объёму выборки 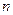называется относительной частотой:

.

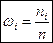Тогда наблюдаемые значения можно сгруппировать в статистический ряд:

Х			…
			…
			…

, .

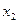
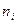
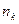
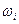
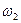
Статистический ряд наглядно можно представить в виде полигона частот (или полигона относительных частот) – ломаной линии, отрезки которой соединяют (,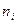) (или (,)).

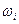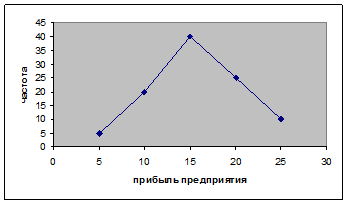
Пример 1. Анализируется прибыль Х предприятий отрасли. Обследованы 100 предприятий. Данные представлены в виде статистического ряда:

Х
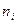
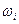
	0,05	0,2	0,4	0,25	0,1

Построить полигон частот.

Решение.

По статистическому ряду можно строить эмпирическую функцию распределения F *(x).

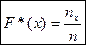, где 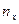- число значений СВ Х < х, 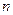- объём выборки.

Свойства F *(x):

1. 0 ≤ ≤ 1.

2. - неубывающая функция, т.е. .

3. .

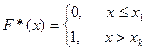Эмпирическая функция распределения является оценкой функции распределения 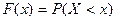, которая называется теоретической функцией распределения.

При большом объёме выборки (или в случае непрерывного признака) её элементы могут быть сгруппированы в интервальный статистический ряд. Для этого все 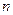наблюдаемых значений выборки разбиваются на k непересекающихся интервалов длиной h (- шаг разбиения). И находят для каждого частичного интервала 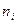- количество наблюдаемых значений СВ Х, попавших в i -й интервал. - относительная частота попадания СВ Х в i -й интервал. Тогда интервальный статистический ряд имеет вид:

			…
			…
			…

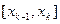
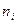
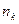
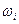
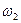
Интервальный статистический ряд наглядно может быть представлен в виде гистограммы частот – столбиковой диаграммы, состоящей из прямоугольников, основаниями которых служат подынтервалы, а высота равна (плотность частоты). Площадь i -го прямоугольника равна 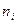, а площадь всей гистограммы частот равна сумме всех частот, т.е. объёму выборки .

Для построения гистограммы относительных частот основание прямоугольника также равно h, а высота 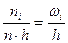. Площадь каждого столбика равна 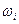. Площадь всей гистограммы относительных частот равна .

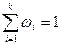На основании гистограммы обычно выдвигается предположение о виде закона распределения исследуемой величины.

Пример 2. Анализируется доход населения. Извлечена выборка объёма 300 единиц. По уровню дохода население подразделяется на 6 групп. Данные сгруппированы в интервальный статистический ряд:

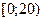
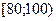
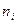
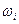
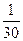
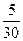
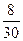
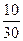
Построить гистограмму относительных частот.

Решение. Шаг h = 20. Разделив относительные частоты на шаг разбиения, получим высоту столбиков.

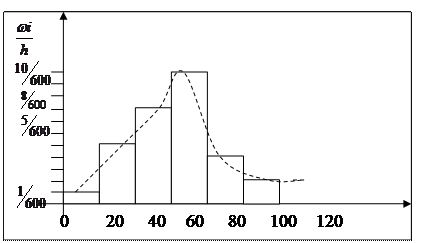
Форма гистограммы в наибольшей степени соответствует нормальному распределению.

Дата добавления: 2014-01-07