Распределение Фишера в регрессионном анализе

Анализ статистической значимости уравнения в целом.

Оценка значимости уравнения регрессии в целом дается с помощью F - критерия Фишера. При этом выдвигается нулевая гипотеза 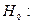о том, что все коэффициенты регрессии, за исключением свободного члена а, равны нулю и, следовательно, фактор х не оказывает влияния на результат y (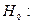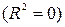или ).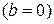

Величина F – критерия связана с коэффициентом детерминации. В случае множественной регрессии:

,

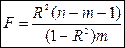где m – число независимых переменных.

В случае парной регрессии формула F – статистики принимает вид:

.

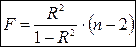При нахождении табличного значения F - критерия задается уровень значимости (обычно 0,05 или 0,01) и две степени свободы: 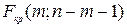– в случае множественной регрессии, 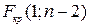– для парной регрессии.

Если 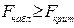, то 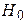отклоняется и делается вывод о существенности статистической связи между y и x.

Если 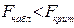, то вероятность уравнение регрессии считается статистически незначимым, не отклоняется.

Замечание. В парной линейной регрессии 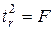. Кроме того, 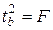, поэтому 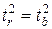. Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

Распределение Фишера может быть использовано не только для проверки гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии, но и гипотезы о равенстве нулю части этих коэффициентов. Это важно при развитии линейной регрессионной модели, так как позволяет оценить обоснованность исключения отдельных переменных или их групп из числа объясняющих переменных, или же, наоборот, включения их в это число.

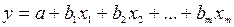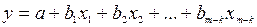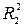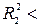
Пусть, например, вначале была оценена множественная линейная регрессия по п наблюдениям с т объясняющими переменными, и коэффициент детерминации равен , затем последние k переменных исключены из числа объясняющих, и по тем же данным оценено уравнение , для которого коэффициент детерминации равен (, т.к. каждая дополнительная переменная объясняет часть, пусть небольшую, вариации зависимой переменной).

Для того, чтобы проверить гипотезу об одновременном равенстве нулю всех коэффициентов при исключённых переменных, рассчитывается величина

,

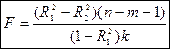имеющая распределение Фишера с 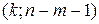степенями свободы.

По таблицам распределения Фишера, при заданном уровне значимости, находят 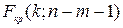. И если 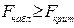, то нулевая гипотеза отвергается. В таком случае исключать все k переменных из уравнения некорректно.

Аналогичные рассуждения могут быть проведены и по поводу обоснованности включения в уравнение регрессии одной или нескольких k новых объясняющих переменных.

В этом случае рассчитывается F – статистика

,

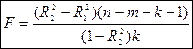имеющая распределение 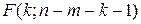. И если она превышает критический уровень, то включение новых переменных объясняет существенную часть необъяснённой ранее дисперсии зависимой переменной (т.е. включение новых объясняющих переменных оправдано).

Замечания. 1. Включать новые переменные целесообразно по одной.

2. Для расчёта F – статистики при рассмотрении вопроса о включении объясняющих переменных в уравнение желательно рассматривать коэффициент детерминации с поправкой на число степеней свободы.

F – статистика Фишера используется также для проверки гипотезы о совпадении уравнений регрессии для отдельных групп наблюдений.

Пусть имеются 2 выборки, содержащие, соответственно, 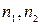наблюдений. Для каждой из этих выборок оценено уравнение регрессии вида 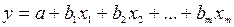. Пусть СКО 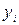от линии регрессии (т.е. 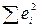) равны для них, соответственно, .

Проверяется нулевая гипотеза 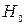: о том, что все соответствующие коэффициенты этих уравнений равны друг другу, т.е. уравнение регрессии для этих выборок одно и то же.

Пусть оценено уравнение регрессии того же вида сразу для всех наблюдений, и СКО .

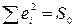Тогда рассчитывается F – статистика по формуле:

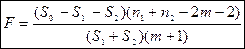
Она имеет распределение Фишера с 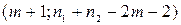степенями свободы. F – статистика будет близкой к нулю, если уравнение для обеих выборок одинаково, т.к. в этом случае 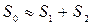. Т.е. если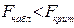 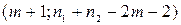, то нулевая гипотеза принимается.

Если же 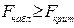, то нулевая гипотеза отвергается, и единое уравнение регрессии построить нельзя.

Дата добавления: 2014-01-07