Пределы государственных расходов

Возможные сочетания частного и государственного производства с частными и государственными поставками

	ЧАСТНЫЕ ПОСТАВКИ	ГОСУДАРСТВЕННЫЕ ПО­СТАВКИ
ЧАСТНОЕ ПРОИЗВОДСТВО	Большинство товаров и услуг на рынке	Примеры: строительство дорог, ремонт, обслуживание оборудо­вания коллективного пользова­ния и т.п.
ГОСУДАРСТВЕННОЕ ПРОИЗВОДСТВО	Государственные пред­приятия и организации	Большинство общественных благ (товаров и услуг)

Предполагается, что в обществе существуют две группы, А и В, функции полезности которых выражаются так: U_a(x_a,g) и Ub(Xb,g). х, и Хь -блага, потребляемые группами А и В соответственно; g - общественное благо, поставляемое государством. Для простоты предполагается, что цены как на частные, так и на общественные блага равны 1. Таким образом, х, и х_ь соответствуют также объемам расходов А и В, a g — государственным расходам.

Общее ограничение ресурсов записывается: у = x_a+Xb+g, где у - сово­купный объем ресурсов, которыми располагает общество.

Оптимума по Парето можно достигнуть, если максимизировать U» для заданного Ub = U ь и при общем ограничении со стороны ресурсов.

Значит:

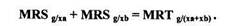
Если учесть линейность бюджетного ограничения (у = х_а+ х_ь+ g), ста­новится понятным, почему MRT g/оы+хь) равно 1 (увеличивая g на 1, полу­чаем на 1 меньше частного блага (х_а + х_ь)).

Получаются те же результаты, что и в любой задаче об оптимуме, только вводится MRS блага g к частным благам в обеих функциях полез­ности.

Вышеуказанное условие позволяет вычислить, с учетом общего ог­раничения ресурсов и априорно установленного значения для Ub в ситуа­ции равновесия, оптимальный объем государственных расходов (и разного рода частных расходов).

Выбор Ub = U ь позволяет выбирать конкретный оптимум на границе общественной эффективности. Особый интерес представляет одно из зна­чений Ub = U ь, а именно - то, которое максимизирует общественное бла­госостояние. Для того, чтобы определить это значение, достаточно решить следующую задачу на поиск максимума:

Получаются уравнения (два условия оптимума и одно общее ограни­чение на ресурсы), то есть, существует единственное решение для трех пе­ременных (х_а, Хь и g). Это решение представляет собой «оптимум оптиму-мов». Легко доказать, что речь идет как раз об оптимуме по Парето [т.е. MRSg,™ + MRSg/_Xb = MRT^^b, ].

Значение, полученное для Ub(Xb,g) в этой точке - то самое, которое в предыдущей задаче следовало взять в качестве исходной точки для Ub, чтобы оптимум, достигнутый при максимизации U, (для Ub = Ub), максимизировал также и W.

Распределение издержек на государственные расходы: анализ Линдаля

В ситуации равновесия принцип альтернативных издержек (условие, необходимое для оптимальной аллокации ресурсов) требует, чтобы каждая единица ресурсов, использованная в общественном секторе, была оплачена по той же цене, по которой за эти ресурсы готов платить частный сектор (с тем, чтобы поставлять частные блага). Величина предельной готовности платить за ресурсы должна быть одинаковой в общественном и в частном секторах. Пассивное (соответственно активное) сальдо бюджета означает, что предельная готовность платить за ресурсы с тем, чтобы поставлять об­щественные блага, ниже (соотв. - выше), чем предельная готовность пла­тить за те же ресурсы с тем, чтобы поставлять частные блага; значит налицо избыток (соотв. - недостаток) общественного блага. Изменение аллокации

ресурсов между двумя секторами, при которой государственные расходы покрываются за счет такой же суммы налоговых сборов с частного сектора, позволило бы добиться улучшений по Парето.

Правило бюджетного равновесия распространяется только на алло­кацию ресурсов в равновесном состоянии - и ничего не говорит о выборе момента, когда следует прибегнуть к нарушению бюджетного равновесия с целью стабилизировать разбалансированную экономику. Более того, при­менение правила должно носить межвременной характер. Если равенство между расходами и доходами должно выполняться в любой момент време­ни, когда дело касается текущих государственных расходов (т.е., имеющих отношение исключительно к покупке услуг или потребительских благ), то дело обстоит иначе, когда под расходами подразумеваются капиталовло­жения. Здесь их объем должен быть равен пересчитанной на настоящий момент сумме налогов, которые в будущем внесут налогоплательщики взамен тех услуг, которые позволят оказать эти капиталовложения в пре­делах каждого периода. Результатом этого будут одновременно и дефицит новых капиталовложений (а, стало быть, и финансирование за счет заем­ных средств или за счет ранее созданных государственных фондов), и до­полнительные платежи по предыдущим капиталовложениям (для погаше­ния долгов, из-за этого возникших - или для того, чтобы учитывать потери предполагаемой выгоды из-за неразмещения собственных фондов, исполь­зуемых на эти цели). Все же для простоты - когда не указывается обратное -мы в дальнейшем будем подразумевать, что государственные расходы включают только текущие расходы. Значит, бюджетное равновесие необ­ходимо будет соблюдать в пределах каждого периода.

Знания того, что совокупный доход должен быть равным расходам, недостаточно, чтобы определять политику бюджетного распределения. Нужно суметь ответить на два вопроса:

1) каков желательный объем государственных расходов?

2) как оптимально распределить затраты в виде налогов на индиви­
дов, пользующихся этими средствами?

Анализ, представленный выше, показал, как главный плановик мог бы ответить на первый вопрос. Для сравнения, анализ Линдаля имеет двойное преимущество он не только отвечает на оба вопроса сразу, но и показывает, как эти ответы можно получить децентрализованно (в резуль­тате переговоров между группами общества, а не при посредстве главного плановика).

1) Диаграмма Линдаля

Общество состоит из двух, однородных групп индивидов, А и В. Их ресурсы до налогообложения составляют соответственно у, и уь (где

У = Уа + Уь)-

Пусть g - это объем государственных расходов, a t- сумма налогов. Бюджет должен быть сбалансирован (тем самым соблюдается принцип альтернативных издержек): g = t.

g на h% платит группа А, а на (l-h%) - группа В. Бюджетные огра­ничения записываются так:

у_а = х_а + h*g и у_ь = x_b + (l-h)*g (где значение h лежит между 0 и 1).

х_а и Хь - количество благ, произведенных частным сектором, кото­рые потребляют соответственно А и В (предполагается, что частные аген­ты не делают сбережений).

На рис. 18а изображен выбор рационально действующего индивида, репрезентативного члена группы А, между благами, поставляемыми обще­ственным и частным секторами. Оптимальное распределение х_а и g для А располагается в точке касания линии бюджетного ограничения для задан­ного h и наиболее высоко расположенной кривой безразличия. В зависи­мости от значения h угол наклона кривой бюджетного ограничения изме­няется, при этом меняется и точка равновесия. Когда h = 1 (А оплачивает 100% государственных расходов), мы попадаем в точку g_ma: бюджетное ограничение х_а = -h*g + у_а имеет наклон - 1, а ордината в начале равна у_а. С уменьшением h, кривая бюджетного ограничения поднимается к гори­зонтальному положению, вращаясь вокруг неподвижной точки у_а. Когда h стремится к нулю, спрос группы на g со стороны группы А стремится к бесконечности (поскольку g больше ничего не стоит для А - при условии, что не возникает насыщения).

Рис. 18. Спрос на благо, поставляемое общественным сектором, и кривая Линдаля для А

8-6036

Местоположение точек равновесия для различных значений h соот­ветствует линии цены, из которой можно вывести кривую спроса на g со стороны А, или «кривую Линдаля для A», g = g_a(h,y_a) (см. рис. 18Ь).

Рис. 19. График Линдаля

Подобным же образом можно вывести и кривую Линдаля для группы В, gb = gb(l - h, у_ь). Если совместить обе кривые на один график (см. рис. 19а, так называемый график Линдаля), можно определить точку равнове-

сия Е. В этой точке, которую называют решение Линдаля обе группы со­гласуются как в отношении государственных расходов (g_e), так и в отно­шении распределения финансирования этих расходов (h_e группой А и 1 - h_e — группой В).3аметим, что:

- вертикальные оси сориентированы в обратном направлении (при
любом увеличении части, оплаченной группой А, на такую же сумму
уменьшается часть, которую оплачивает В);

- горизонтальные оси в том же направлении, так как группа А потре­
била такое же количество расходов g, что и В. Это происходит по следую­
щей причине: в отличие от ситуации с частными благами, индивиды кон­
курируют между собой не за потребление g, а только за его финансирова­
ние. Следствием этого отсутствия конкуренции является, однако, согласо­
ванность объемов поставки (g_a и g_b равны);- кривые Линдаля зависят от
доходов рассматриваемых групп. Если, например, у_а возрастает, то кривая
Линдаля для группы А смещается вправо - при условии, что благо (товар
или услуга) g не менее качественный в отношении группы А, По той же
закономерности, если уь убывает, то график уь смещается влево (для того
же самого значения 1-h спрос группы В на g меньше - опять же при усло­
вии, что благо g для нее не является менее качественным - см. рис.
19Ь).Если предположить, что каждая из групп располагают исчерпываю­
щей информацией о своей кривой спроса, можно полагать, что точка рав­
новесия будет достигнута в процессе переговоров. Возьмем ситуацию, ко­
гда равновесие нарушено: на рис. 19 объявлен возможный объем государ­
ственных расходов. Группа А согласна платить h' и платит (1-h)'. Вопрос
состоит в том, что сумма h' и (1-h)' меньше 1. Группы А и В не готовы
финансировать весь объем g'. Тогда будет объявлен меньший объем рас­
ходов, чтобы приблизить к единице сумму значений готовности платить.
После некоторого числа переговоров такого рода, при условии конвер­
гентного характера процесса, точка равновесия g_e будет достигнута, и это
решение будет соответствовать оптимуму по Парето, т.е.

3) Решение Линдаля и максимум общественного благосостояния.

Каждому распределению доходов (каждому значению у_а° и Уь = у — у_я°) решение Линдаля ставит в соответствие различные оптиму-мы по Парето. Значит, можно вычислять значения у_а* и у_ь* = у - у_а*, по­зволяющие при помощи переговоров по Линдалю получать такой оптимум по Парето, который бы максимизировал функцию общественного благо­состояния, W. Чтобы перейти от начального распределения к этому, опти­мальному распределению, необходимо перераспределение. Обозначим по­следнее через tr:

Дата добавления: 2014-01-07