Автоматы с магазинной памятью (MП-автоматы)

Рассмотрим понятие автомата с магазинной памятью – тип распознавателя, представляющий собой естественную модель синтаксических анализаторов контекстно-свободных языков. Автомат с магазинной памятью – это односторонний недетерминированный распознаватель, в потенциально бесконечной памяти которого элементы информации хранятся и используются так же, как патроны в магазине автоматического оружия, т.е. в каждый момент доступен только верхний элемент магазина. Распознаватель этого типа изображен на рисунке ниже.

Будем представлять магазин (или магазинный список, или магазинную ленту) в виде цепочки символов, причем верхним элементом магазина будем считать самый левый или самый правый символ цепочки в зависимости от того, что удобнее в данной ситуации. Пока будем считать верхним самый левый символ цепочки, представляющей магазинный список.

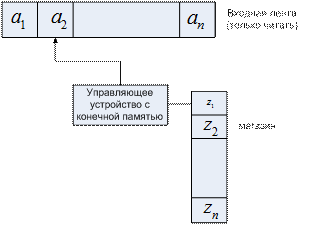
Рис. 1. Автомат с магазинной памятью

Определение: Автомат с магазинной памятью (МП-автомат) – это упорядоченная семерка вида

,

где

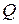-конечное множество состояний автомата;

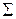-конечный входной алфавит;

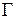-конечный алфавит магазинных символов;

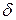-множество функций переходов автомата (отобра­жение множества вида 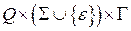в множество конечных подмножеств множества );

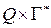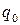-начальное состояние автомата или управляющего устройства ();

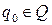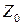-начальный символ магазина (символ, находящийся в магазине в начальный момент времени );

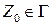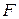-множество заключительных состояний автомата ().

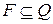Определение: Конфигурацией автомата с магазинной памятью (МП-автомата) называется упорядоченная тройка вида

,

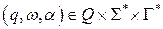где

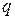-текущее состояние автомата;

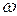-неиспользованная или нерассмотренная часть входной цепочки (первый или самый левый символ находится над считывающей головкой), если 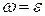, то входная цепочка уже прочитана;

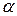-содержимое магазина (будем считать, что левый символ цепочки – это вершина стека), если 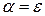, то магазин считается пустым.

Определение: Тактом работы автомата с магазинной памятью 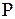будем называть бинарное отношение вида

,

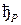то есть переход из одной конфигурации в другую

,

если 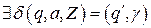, где, , , , .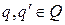

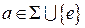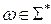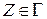Индекс в отношении пишут для идентификации, к какому автомату относится данное бинарное отношение.

Соглашение: Далее будем считать эквивалентными обозначения 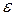- пустая цепочка и 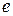- пустой символ

Определение: Если 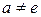, то это отношение говорит о том, что МП-автомат находясь в состоянии 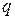и имея 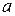в качестве текущего входного символа, расположенного над входной головкой, а 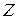- в качестве верхнего символа магазина, может перейти в новое состояние , сдвинуть входную головку на одну ячейку вправо и заменить верхний символ магазина цепочкой 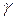магазинных символов. Это отношение называется непустым тактом работы МП-автомата.

Если 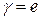, то верхний символ удаляется из магазина, и тем самым магазинный список сокращается.

Определение: Если 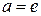, тогда входной символ из цепочки не считывается, но автомат может перейти в другое состояние и изменить содержимое магазина, такие такты называются 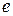-тактами.

Работа автомата заканчивается, если магазин пуст.

Определение: Начальной конфигурацией автомата будем называть тройку вида

,

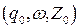где

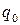- начальное состояние ();

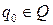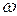- входная цепочка ();

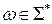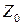- начальный символ магазина ().

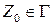Определение: Заключительной конфигурацией автомата будем называть тройку вида

,

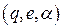где

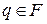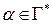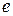, , -пустой символ.

Определение: Цепочка 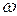допускается МП-автоматом , если имеет место бинарное отношение вида

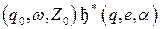, (1)

где

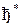- последовательность тактов работы автомата;

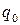- начальное состояние автомата;

, , , .

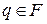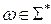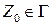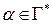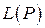Определение: Языком определяемым (или допускаемым) автоматом (обозначается ) называется множество цепочек 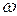, допускаемых автоматом , т.е.

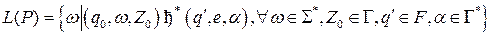
Пример:

Построить МП-автомат, заданный следующим множеством

;

.

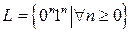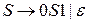Решение:

Автомат будет выглядеть следующим образом

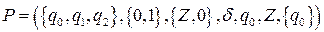
Построим функции перехода для МП-автомата (интуитивным способом)

;

;

;

;

;

.

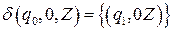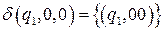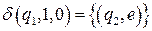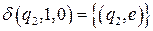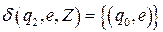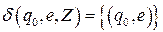Домашнее задание: Записать последовательность работы тактов МП-автомата для двух входных цепочек

;

.

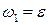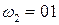Домашнее задание: Написать другие функции перехода МП-автомата (интуитивным способом), то есть написать свой МП-автомат.

Пример:

Построить МП-автомат, заданный следующим множеством

;

;

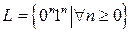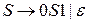и построить последовательность тактов работы МП-автомата для цепочки

.

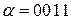Решение:

Построим функции перехода для МП-автомата (интуитивным способом)

;

;

;

;

;

,

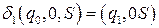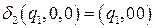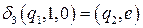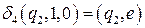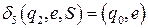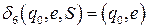где

, , , .

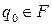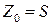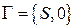Теперь построим последовательность тактов работы автомата для цепочки

.

.

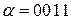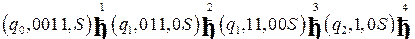
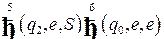Определение: Расширенным МП-автоматом назовем семерку вида

,

где

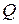- конечное множество состояний автомата;

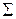- конечный допустимый входной алфавит;

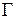- алфавит магазинных символов;

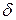- отображение множества 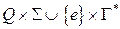в множество конечных подмножеств множества ;

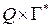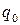- начальное состояние автомата ();

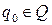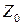- начальный символ магазина (символ, находящийся в магазине в начальный момент времени );

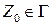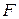- множество заключительных состояний ().

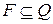Определение: Конфигурация расширенного МП-автомата - это упорядоченная тройка вида

.

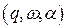Определение: Начальной конфигурацией расширенного МП-автомата будем называть тройку вида

,

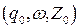где

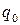- начальное состояние;

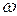- входная цепочка;

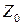- начальный символ магазина.

Определение: Заключительной конфигурацией расширенного МП-автомата будем называть тройку вида

,

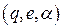где

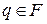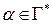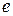, , -пустой символ.

Определение: Цепочка 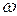допускается расширенным МП-автоматом , если имеет место бинарное отношение вида

,

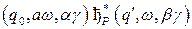где

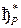- последовательность тактов работы расширенного МП-автомата ;

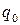- начальное состояние автомата;

, , , , .

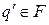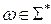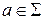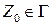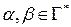Определение: Языком, определяемым расширенным МП-автоматом , является множество вида

.

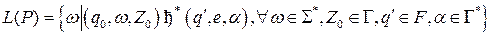Замечание: Заметим, что в отличие от обычного МП-автомата расширенный МП-автомат обладает способностью продолжать работу и тогда, когда магазин пуст.

Пример:

Построить расширенный МП-автомат, заданный следующим множеством

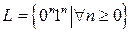
и построить последовательность тактов работы расширенного МП-автомата для цепочки

.

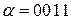Решение:

Приведем два варианта решения данного примера.

Вариант №1.

Расширенный МП-автомат будет выглядеть следующим образом

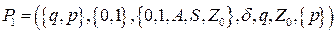
Правила грамматики 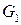имеют следующий вид

.

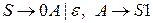Построим функции перехода для расширенного МП-автомата (интуитивным способом)

,

,

,

,

,

.

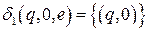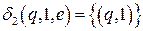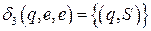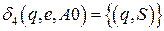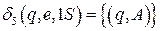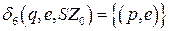Теперь построим последовательность тактов работы автомата для цепочки

.

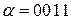Последовательность тактов работы расширенного МП-автомата имеет вид

.

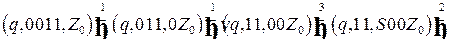
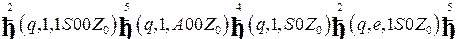
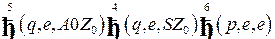Вариант №2.

Расширенный МП-автомат будет выглядеть следующим образом

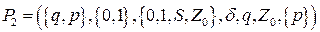
Правила грамматики 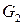имеют следующий вид

.

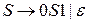Построим функции перехода для расширенного МП-автомата (интуитивным способом)

,

,

,

,

.

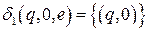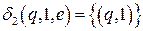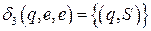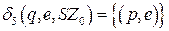Теперь построим последовательность тактов работы расширенного МП-автомата для цепочки

.

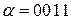Последовательность тактов работы расширенного МП-автомата имеет вид

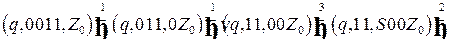
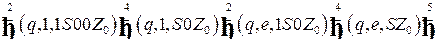
Дата добавления: 2014-01-07